UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreTetrominoes, in general, are classified into different types based on the alignment of the four-unit squares present in it. They are orthogonal.
Based on the alignments the tetrominoes are classified into five base types namely,
- Straight-Tetromino
- Square-Tetromino
- \(L\)-Tetromino
- \(Z\)-Tetromino
- \(T\)-Tetromino
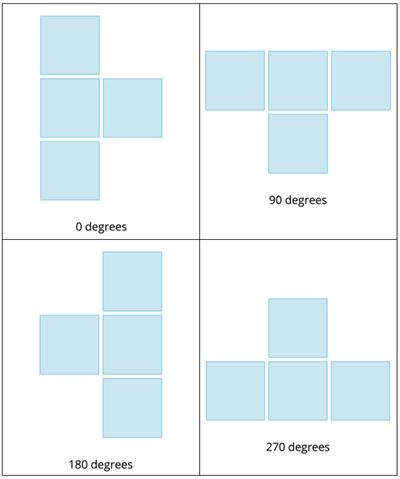
Rotational Properties of Tetrominoes:
- We represent these five tetrominoes in various ways based on their angle of rotation.
- When we rotate the tetrominoes in \(90\) degrees clockwise or anti-clockwise direction, it begins to produce different projections of their base types.
- Even if we rotate tetrominoes to different angles, they remain at their same base type.
- Some tetrominoes exhibit Rotational-Symmetry.
Rotational-Symmetry is the property a shape has when it looks the same after some rotation by a partial turn, and it is the number of distinct orientations in which it seems the same for each rotation.
The different tetrominoes obtained after angular rotations are given below:
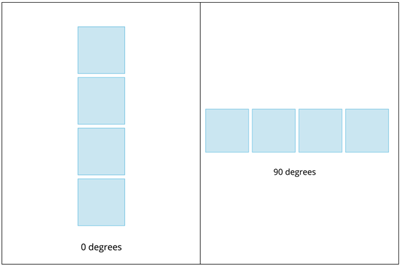
Straight-Tetromino:
- The Straight-Tetromino exhibits \(2\)fold Rotational-Symmetry. That is, the Straight-Tetromino obtains the same shape \(2\) times while undergoing a rotation of \(90\) degrees till it reaches the original shape.
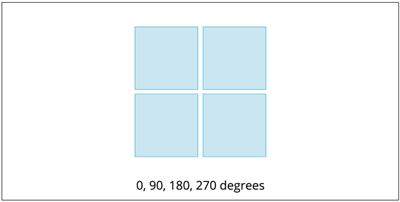
Square-Tetromino:
- The Square-Tetromino exhibits \(4\)fold- Rotational-Symmetry. That is, the Square-Tetromino obtains the same shape \(4\) times while undergoing a rotation of \(90°\) till it reaches the original shape.
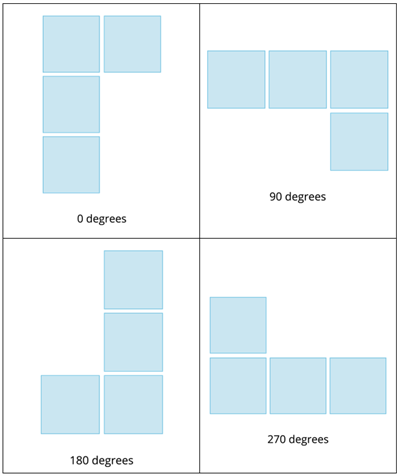
L-Tetromino:
Z-Tetromino:
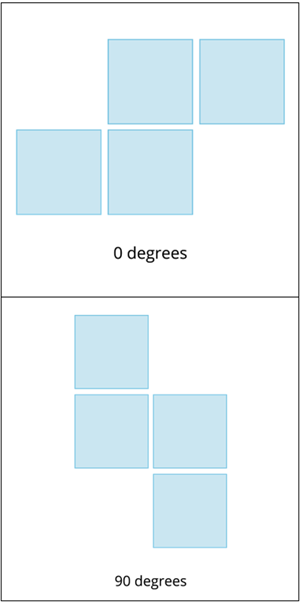
T-Tetromino:
Register for free to see more content