PDF chapter test TRY NOW
ஒரு உயரமான கொள்கலன் திரவத்தால் நிரப்பப்படுகிறது, இதனால் அது ஒரு திரவத்தம்பத்தை உருவாக்குகிறது.
அதன் குறுக்கு வெட்டுப்பரப்பளபை \(A\) என்க.
திரவத்தின் அடர்த்தி \(\rho\) ஆல் குறிக்கப்படுகிறது, மேலும் திரவத்தம்பத்தின் உயரம் \(h\) ஆகும்.
வேறுவிதமாகக் கூறுவதானால், மேல்-நிலை மேற்பரப்பில் இருந்து நீரின் ஆழம் \(h\) ஆகும்.
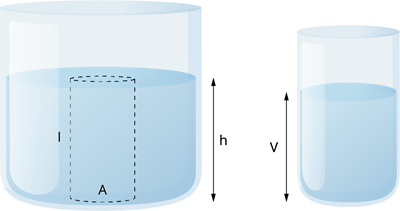
திரவத்தம்பத்தினால் ஏற்படும் அழுத்தம்
திரவத்தம்பத்தின் அடிப்பகுதியிலுள்ள உந்து விசையானது திரவத்தின் எடைக்கு சமம் என்பதை நாம் அறிவோம். ஆகையால்,
திரவத்தின் நிறையானது திரவத்தின் பருமனை அதன் அடர்த்தியால் பெருக்கினால் கிடைக்கும். எனவே:
எனவே, திரவத்தின் பருமன்:
சமன்பாடு \(3\) இல் \(2\) பிரதியிட:
நிறை,
சமன்பாடு (\(4\) ஐ, \(1\) இல் பிரதியிட:
இப்போது, அதை அழுத்த சூத்திரத்தில் பயன்படுத்தவும்.
எனவே,
மேலே உள்ள சமன்பாடு ஒரு திரவத் தம்பத்தினால் ஏற்படும் அழுத்தம் ஆனது ஆழம், திரவத்தின் அடர்த்தி மற்றும் ஈர்ப்பு விசையின் முடுக்கம் ஆகியவற்றால் தீர்மானிக்கப்படுகிறது என்பதைக் காட்டுகிறது.
இருப்பினும், அழுத்தத்திற்கான இறுதி சமன்பாடு பகுதி \(A\) என்ற சொல்லைக் கொண்டிருக்கவில்லை. எனவே, ஒரு திரவத்தில் அழுத்தம் ஆழத்தை மட்டுமே சார்ந்துள்ளது.
Example:
\(0.9\) மீ திரவத்தம்பையால் செலுத்தப்படும் நீரின் அழுத்தத்தைக் கணக்கிடுங்கள். (நீரின் அடர்த்தி, \(ρ_w\ =\) \(1000\) கிகி மீ\(^{-3}\)
தீர்வு:
திரவத்தம்பையின் உயரம் அல்லது ஆழம் (\(h\)) \(=\) \(0.9\) மீ
நீரின் அடர்த்தி (\(ρ\)) \(=\) \(1000\) கிகிமீ\(^{-3}\)
