PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoLet us learn how to solve real-life situations based on the angle of depression.
Example:
1. A man observes the ball, which is at a distance of \(1.5 \ m\) from him. If the angle of depression is \(45^{\circ}\), then find the height of the man.
Solution:
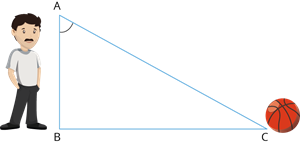
Let \(AB\) denote the height of the man and \(BC\) denote the distance of the man from the ball.
From the given data, we have:
\(\theta = 45^{\circ}\), and \(BC = 1.5 \ m\)
To find: The height of the man (\(AB\)).
Explanation:
In the right \(\triangle ABC\), \(tan \ \theta = \frac{BC}{AB}\)
\(tan \ 45^{\circ} = \frac{1.5}{AB}\)
\(1 = \frac{1.5}{AB}\)
\(AB = 1.5 \ m\)
Therefore, the height of the man is \(1.5 \ m\).
2. A man observes a ball which is at a distance of \(1.2 \sqrt{3} \ m\) from him. If the height of the man is \(1.2 \ m\), then find the angle of depression.
Solution:
Let \(AB\) denote the height of the man and \(BC\) denote the distance of the man from the ball.
From the given data, we have:
\(AB = 1.2 \ m\), and \(BC = 1.2 \sqrt{3} \ m\)
In the right angled triangle \(ABC\), \(tan \ \theta = \frac{BC}{AB}\)
\(tan \ \theta = \frac{1.2 \sqrt{3}}{1.2}\)
\(tan \ \theta = \sqrt{3}\)
\(\theta = 60^{\circ}\)
Therefore, the angle of depression is \(60^{\circ}\).
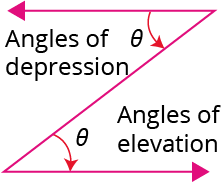
Important!
The angle of elevation and angle of depression are equal because they are alternate angles.
Register for free to see more content