Perimeter of a triangle — lesson. Mathematics CBSE, Class 6.

UPSKILL MATH PLUS

Learn Mathematics through our AI based learning portal with the support of our Academic Experts!

Now, we shall find the perimeter of an equilateral triangle.

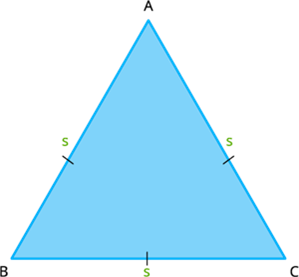
Let \(ABC\) be an equilateral triangle with sides of equal length \(s\) \(units\).

Then, the perimeter of the triangle \(ABC\) is given by:

Perimeter of the triangle \(=\) Product of \(3\) sides and its side length

Perimeter \(P = AB+BC+CA\) \(units\)

\(P = s+s+s\) \(units\)

\(P = 3s\) \(units\)

Therefore, the perimeter of an equilateral triangle is the product of \(3\) sides and the side length.

Example:

1. The side length of an equilateral triangle is \(9 \ cm\). Find the perimeter of an equilateral triangle.

Solution:

The side length of an equilateral triangle is \(s = 9\) \(cm\).

Perimeter \(= 3s\), where \(s\) is the length of three equal sides.

Substituting the value of \(s\) in the above formula, we have:

Perimeter \(= 3 \times 9\) \(cm\)

Perimeter \(= 27\) \(cm\)

Therefore, the perimeter of an equilateral triangle is \(27 \ cm\).

Did you find an error?

4. Perimeter of a triangle