PDF chapter test TRY NOW
Distributive property:
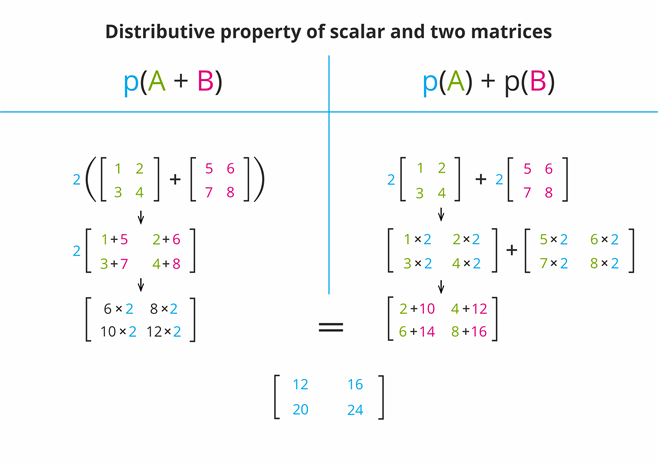
1. Distributive property of scalar and two matrices - \(p(A+B) = pA+ pB\)
Let \(A\), and \(B\) be \(m×n\) matrices and \(p\) and \(q\) be two non-zero scalars (numbers).
Example:
Consider the matrices \( A = \begin{bmatrix}
1 & 2 \\
3 & 4
\end{bmatrix}, B = \begin{bmatrix}
5 & 6\\
7 & 8
\end{bmatrix}\) and \(p = 2\) then verify \(p(A+B) = pA+ pB\).
1 & 2 \\
3 & 4
\end{bmatrix}, B = \begin{bmatrix}
5 & 6\\
7 & 8
\end{bmatrix}\) and \(p = 2\) then verify \(p(A+B) = pA+ pB\).
Solution:
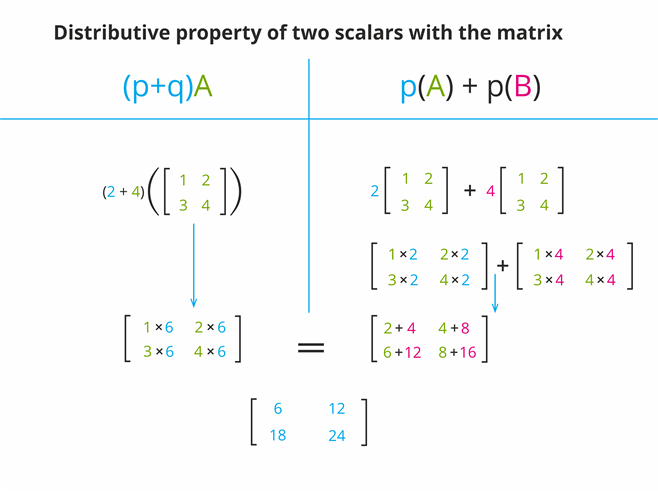
2. Distributive property of two scalars with a matrix - \((p +q)A = pA +qA\)
Example:
Let's take the same matrices to prove \(A = \begin{bmatrix}
1 & 2 \\
3 & 4
\end{bmatrix}\) to prove \((p +q)A = pA +qA\). Where \( p = 2\) , and \( q = 4\).
1 & 2 \\
3 & 4
\end{bmatrix}\) to prove \((p +q)A = pA +qA\). Where \( p = 2\) , and \( q = 4\).
Solution: