UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreIn \(1972\), Terrel Trotter, Jr., then a math teacher in Urbana Illinois, published an article called Normal Magic Triangles.
To setting up the magic triangle, we require a little knowledge of arithmetic.
Six Circle Magic Triangle: To place the numbers \(1\), \(2\), \(3\), \(4\), \(5\), \(6\) in the circles so that the sums of the three numbers on either side of the triangle(side length of the triangle) are the same.
The only four possible solution for this triangle problems are as follows:
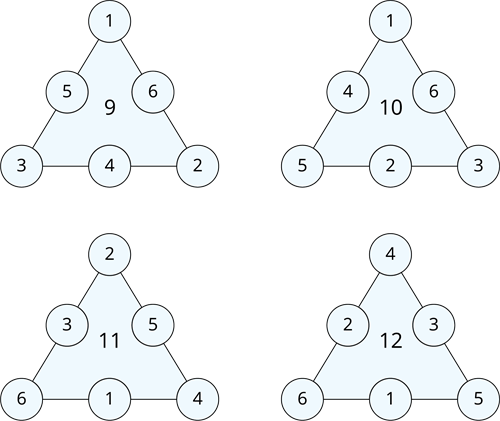
Technique to make the side length as \(9\):
- Keep the lower numbers(\(1\), \(2\) and \(3\)) at the corners of the triangle.
- Place the largest number(\(6\)) in between the two smallest(\(1\) and \(2\)) corner arrangements.
- The remaining middle numbers will be \(4\) and \(5\).
- To reach side length as the least sum \(9\) we have to place \(4\) between \(3\) and \(2\) and place \(5\) between \(1\) and \(3\).
- Thus, we made the magic triangle with the least side length of \(9\) units.
Technique to make the side length as \(11\):
- Keep the even digits of (\(2\), \(4\) and \(6\)) at the corners of the triangle.
- Place the second larger number(\(5\)) in between the two smallest(\(2\) and \(4\)) corner arrangements.
- The remaining numbers will be \(1\) and \(3\).
- To reach side length as \(11\) we have to place \(1\) between \(6\) and \(4\) and place \(3\) between \(6\) and \(2\).
- Thus, we made the magic triangle with the least side length of \(11\) units.
Now try to establish the techniques for the other two magic triangles and explore its outcomes.
Important!
Rotations and reflections of the magic triangle are not considered as the unique solutions. Each of the magic triangle solution has two rotations and each of these has one reflection. There are \(6\) possible orientation for each solution.
Let us see all the \(6\) possible orientation of the side length \(9\).
Register for free to see more content