UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn morePrime factorization is to write the composite number as a product of its prime factors.
Let us find the prime factor for \(12\).
\(12 = 4 \times 3\)
\(4\) can be written as \(2 \times 2\).
\(12 = 2 \times 2 \times 3\)
Therefore, the prime factor of \(12\) is \(2 \times 2 \times 3\).
There are two ways to find the prime factor.
1. Factor tree method
2. Division method
Factor tree method
Let's see the example using factor tree method.
Example:
Find the prime factor of \(48\) using the factor tree method.

Prime factor of \(48\) \(=\) \(8 \times 6\).
Prime factor of \(8\) \(=\) \(4 \times 2 = 2 \times 2 \times 2\).
Prime factor of \(6\) \(=\) \(3 \times 2\).
The ending prime numbers are the prime factors.
Therefore, the prime factor of \(48\) \(=\) \(2 \times 2 \times 2 \times 2 \times 3\).
Division method:
Step 1: Write the given number.
Step 2: Start with the lowest prime number, which exactly divides the given number.
Step 3: Write that lowest prime number on the left side of the given number.
Step 4: Write down the quotients in the next line of the given number.
Step 5: Repeat the process until you get \(1\) as a quotient.
Step 6: The prime numbers you obtained on the left side of the given number is prime factors.
Example:
Find the prime factor of \(27\) using division method.
Write a pair of factors.
\(27 = 9 \times 3\)
Now further factorize the composite factor \(9\) as \(3\) and \(3\).
Repeat the process till you get the prime factors of all the composite factors.
Since the last number \(3\) is a prime number, we cannot factorize it further.
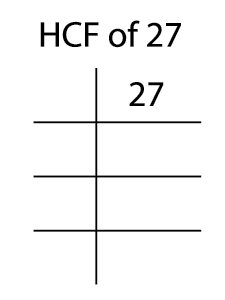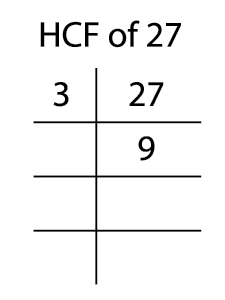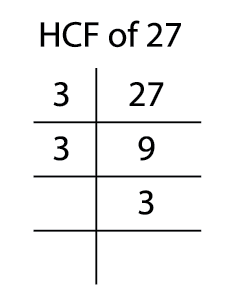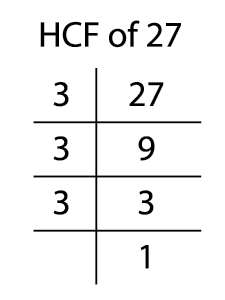
Therefore, the prime factor of \(27\) \(=\) \(3 \times 3 \times 3\).