PDF chapter test TRY NOW
Like and unlike:
When you visit a library, you can see that the books are arranged separately according to the genre of the book.
The mathematics books and history books of the same kind are kept as separate racks in a different place.
This means that all mathematics books are like, and history books are unlike each other.
Similarly, we can group the same kind of terms in an algebraic expression.
Example:
Now take a look at this,
here this expression has \(5\) terms and out of \(3\) terms have the same variable factor that is \(x\).
So now we can say that the are like terms.
And the terms have a different variable factor.
That is the terms \(10x\) have \(x\) as a variable factor, the term \(2y\) have \(y\) as a variable factor, and the term \(6z\) have \(z\) as a variable factor.
So this kind of terms is called as, unlike terms.
Now let's see some examples with a definition for proper understanding.
Like terms:
The terms which have the same variable factor that is called like terms.
Example:
Like terms are:
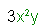 | and | 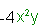 |
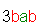 | and | 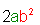 |
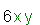 | and | 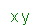 |
\(-3\) | and | \(10\) |
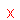 | and |  |
Here we have to care about only the variable is same or not irrespective of the arithmetic operation\((+, -)\)
Unlike terms:
The terms which have the different variable factor that is called as, unlike terms.
Example:
Unlike terms are:
