
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoAltitude position differs for various types of triangle. Let us discuss its types:
- Acute angled triangle
- Right angled triangle
- Obtuse angled triangle
- Equilateral triangle and
- Isosceles triangle
Altitude in acute angled triangle:
All three altitude lies inside the triangle.
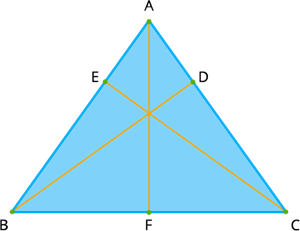
Here \(ABC\) is an acute-angled triangle and \(AF, BD\) and \(CE\) are the altitudes of the triangle \(ABC\) and all three altitudes lies inside the triangle.
Altitude in right angled triangle:
The altitude perpendicular to the hypotenuse lies inside the triangle, but the other two altitudes are the legs of the triangle.

Here \(ABC\) is a right-angled triangle, and \(BD\) is the altitude perpendicular to the hypotenuse lies inside the triangle, but the other two altitudes \(AB\) and \(BC\) are the legs of the triangle.
Altitude in obtuse angled triangle:
The altitude connected to the obtuse vertex lies inside the triangle, but the two altitudes connected to the acute vertices are outside the triangle.
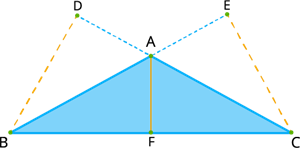
Here \(ABC\) is an obtuse-angled triangle, and \(AF\) is the altitude connected to the obtuse vertex lies inside the triangle, but the other two altitudes \(BD\) and \(CE\) connected to the acute vertices are outside the triangle.
Altitude in equilateral triangle:
The altitudes of an equilateral triangle bisect its base and the opposite angle.
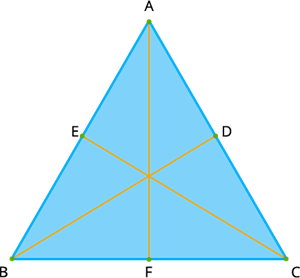
Here \(ABC\) is an equilateral triangle and \(AF, BD\) and \(CE\) are the altitudes lie inside the triangle as it an acute-angled triangle. Also, altitudes of an equilateral triangle bisect its base and the opposite angle. For an equilateral triangle, the all three lines \(AF, BD\) and \(CE\) are altitudes, medians as well as angle bisector of the triangle \(ABC\).
Altitude in isosceles angled triangle:
The altitudes of an isosceles triangle bisect its unequal base and the opposite angle. But this will not suit for other \(2\) altitudes.

Here \(ABC\) is an isosceles triangle and \(AF, BD\) and \(CE\) are the altitudes of the triangle. Also, altitudes of an isosceles triangle bisect its unequal base \(BC\) and the opposite angle \(A\), but this will not be true for the equal bases \(AC\) and \(AB\) and the opposite angles \(B\) and \(C\).