PDF chapter test TRY NOW
In any triangle, the difference in the length of any two sides of a triangle is always lesser than the third side.
In here, the inequalities are as follows:
\(a - b < c\)
\(b - c < a\) and
\(c - a < b\)
Example:
Consider the triangle\(ABC\) whose sides measures are \(AB = c = 3 cm, BC = a = 4 cm\) and \(AC = b =5 cm\).
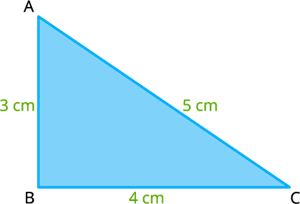
Let's check the triangle inequality for the triangle \(ABC\),
\(a - b = 4 - 5 = -1 < 3 = c\)
\(b - c = 5 - 3 = 2 < 4 = a\) and
\(c - a = 3 - 4 = -1 < 5 = b\)
Important!
Suppose \(a, b\) and \(c\) are the sides of a triangle with \(a\) and \(b\) are known sides and \(c\) is unknown. Let's use the triangle inequality to find the third side \(c\). As the sum of two sides\((a+b)\) of a triangle is always greater than the third side\((c)\), and difference of two sides\((a-b)\) of a triangle is always lesser than the third side\((c)\), the length of the third side\((c)\) must lie between difference\((a-b)\) and sum\((a+b)\).
