UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreWhile, division of 2 integers, depending upon the sign of the two or more than two numbers involved, the answer can change.
A negative number divided by another negative number will result in a positive number \((-ve)/(-ve)=+ve\).
Example:
1. \(=\) 2
2. \(=\) 3
3. \(=\) 4
4. \(=\) 10
In division operation, when numerator and denominator have different signs, the result will have a negative sign \((-ve)/(+ve) = -ve\).
Example:
1. \(=\) −20
2. \(=\) −7
3. \(=\) −100
4. \(=\) −10
In division operation, when both numerator and denominator are positive numbers, the result will also be positive \((+ve)/(+ve) = +ve\).
Example:
1. \(=\) 7
2. \(=\) 34
3. \(=\) 90
4. \(=\) 5
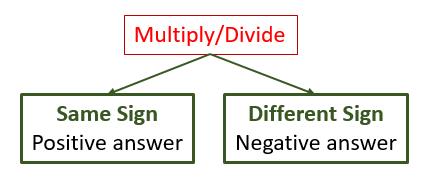
While, multiplying 2 integers, depending upon the sign of the two or more than two numbers, the answer can change.
In multiplication operation, if anyone of the numbers is negative, then the result will have a negative sign \((+ve) × (-ve) = -ve\).
Example:
1.303 \(×\) −5 \(=\) −1515
2.894 \(×\) −67 \(=\) −59898
3. 9 \(×\) −67 \(=\) −603
In multiplication operation, when both the numbers are negative, then the result will have a positive sign \((-ve)×(-ve) = +ve\). This is in accordance with Euler, a mathematician who proved, \((-1)×(-1)=+1\).
Example:
1. \((-9) × (-10) = 90\)
2. \((-12) × (-6) = 72\)
3. \((-10) × (-10) = 100\)
4. \((-5) × (-5) = 25\)
In multiplication, when both the numbers are positive, the result will be a positive sign \((+ve) × (+ve) =+ve\)
Example:
1. \(12× 10 = 120\)
2. \(10 × 6 = 60\)
3. \(10 × 5 = 50\)
4. \(8 × 6 = 48\)
Any integer \(/\) \(0 =\) infinite or cannot be determined because still, researches are going on to find out what will be the result when an integer is
divided by zero, an approximation cannot be taken out.
Example:
1. \(=\) infinite or cannot be determined.
2. \(=\) infinite or cannot be determined.
Any integer \(×\) \(0 = 0\). Irrespective of nature and sign of integer, when an integer is multiplied by zero, the result is \(0\).
Example:
1. \(40 × 0 = 0\)
2.894 \(×\) \(0\) \(=\) 0