PDF chapter test TRY NOW
A quadrilateral whose opposite sides are parallel in pairs is called a parallelogram.
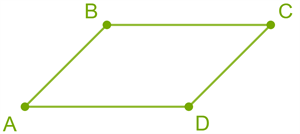
Properties of a parallelogram
The opposite sides of the parallelogram are of equal length in pairs. \(AB = DC\) \( BC = AD\) 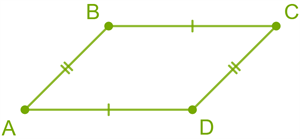 |
The opposite angles of a parallelogram are equal in size. \(A =\)\(C\) \(B =\)\(D\) 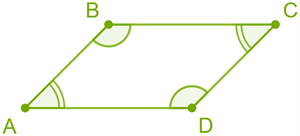 |
The parallelogram divides at the intersection of the diagonal in half. \(BO = OD\) \(AO = OC\) 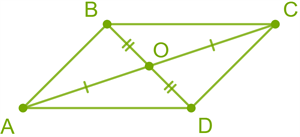 |
The diagonal of parallelogram divides it into two equal triangles. Triangles \(ABC\) and \(CDA\) are equal. 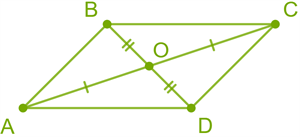 |
The sum of the angles on each side of the parallelogram is \(180\) degrees. \(A +\)\(D = 180\) degrees 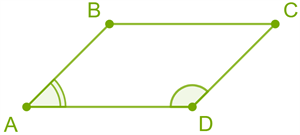 |
The transverse angles at the diagonal are the same. \(BAC =\)\(ACD\) \(BCA =\)\(CAD\) 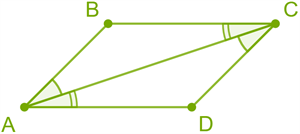 |
