PDF chapter test TRY NOW
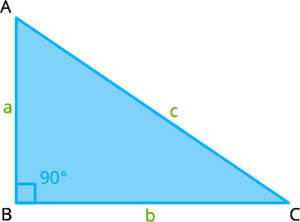
Right Angle triangle: A triangle where one of its interior angles is a right angle \(90°\).
Area:
(Area\) \(A = \) \(1/2(b × h)\)
Thus, height of triangle \(h =\) \(Area × 2 / b\)
And, base of triangle \(b =\) \(Area × 2 / h\)
where \(h\) is denoted as height.
where \(b\) is denoted as base.
Perimeter:
\(a²\) \(+\) \(b²\) \( = c²\)
\(a\), \(b\) are the lengths of the other two sides.
where \(c\) is the length of the hypotenuse.
Sides:
- The two sides that are not the hypotenuse.
- They are the two sides making up the right angle itself.
Hypotenuse:
- The side opposite the right angle.
- This will always be the longest side of a right triangle.
Properties:
- If the two sides that include the right angle are equal in length(\(AB\) and \(BC\)). then it said to be an isosceles triangle.
- The hypotenuse (the side opposite the right angle) is always longer than either of the other two sides.so it can never be an equilateral triangle.
Isosceles triangle: A triangle which has two of its sides equal in length.

Area:
\(Area\) \(A = \) \(1/2(b × h)\)
Thus, height of triangle \(h =\) \(Area × 2 / b\)
And, base of triangle \(b =\) \(Area × 2 / h\)
where \(h\) is denoted as height.
where \(b\) is denoted as base.
Perimeter:
\(P =\) \(2a + b\)
\(a\) are the lengths of the two equal sides
\(b\) are the lengths of the other sides.
Properties:
- The 'base' of the triangle is referred to the unequal side of an isosceles triangle.
- The base angles of an isosceles triangle are always equal. (\(∠ABC\) and \(∠ACB\) are always the same)
- The altitude is a perpendicular distance from the base to the topmost vertex.
- When the \(3rd\) angle is a right angle, it is called a "right isosceles triangle".
- If all three sides are the same length it is called an equilateral triangle. Obviously all equilateral triangles also have all the properties of an isosceles triangle.
Important!
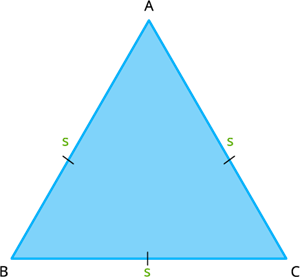
Equilateral Triangle: A triangle which has all three of its sides equal in length.
Area:
\( Area\) \(A = √3/4\)\( s² \)
where \(s² \) denotes sides of the triangle.
Perimeter:
\(perimeter\) \(P = a + b + c \) or \(P = s + s + s\)
\(a\), \(b\), \(c\) are the lengths of the three equal sides.
or
\(s\) are the lengths of the three equal sides.
Properties:
- All three angles of an equilateral triangle are always \(60°\).Hence, \(∠ABC\), \(∠CAB\) and \(∠ACB\) are always the same. Since the angles are the same and the internal angles of any triangle always add to \(180°\), each is \(60°\).
- An equilateral triangle is one in which all three sides are congruent (same length). Because it also has the property that all three interior angles are equal.
