PDF chapter test TRY NOW
The experiment requires a cell, nichrome wire, key, an ammeter, and a plug key.
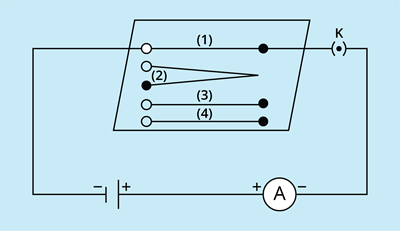
Experimental set-up
- Connect the cell, ammeter and key in series using the nichrome wire of length (\(l\)).
- Close the key.
- Note down the current value in the ammeter.
- Now, replace the nichrome wire with another one of the same thickness but twice the length, (\(2l\)) [point (\(2\))].
- Again, note the current value in the ammeter.
- Now, replace the nichrome wire with another one with more thickness of the same length (\(l\)) [point (\(3\))]. [NOTE: A thicker metallic wire has a large cross-sectional area.]
- Again, note the ammeter reading.
- In the given circuit, connect a copper wire instead of a nichrome wire [point (\(4\))].
- Maintain the same length and the area of cross-section as that of the first nichrome wire [point (\(1\))].
- Now, note down the current value in the ammeter.
Is there any difference in the current values in all cases? Does the current depend on the length of the conductor or the area of cross-section of the wire used?
From the above experiment, it can be observed that
- The current value decreases to half when the length of the wire is doubled.
- The reading is increased when a thicker wire of the same length and material is used.
- When a wire of different materials of the same length and the area of cross-section are used, the reading changes.
Let us discuss and derive this in detail.
Factors affecting resistance:
The resistance of a material or a conductor depends on three factors. They are,
- Nature of conductor
- Length of conductor
- Area of a cross-section of the conductor
Nature of a conductor:
The resistance of a conductor varies for different types of materials, depending on their nature.
In the electrical experiment, it can be easily proved that the conductor's resistance (\(R\)) is directly proportional to its length (\(L\)) and inversely proportional to its area of cross-section (\(A\)).
Register for free to see more content