PDF chapter test TRY NOW
Consider any two objects or balls \(A\) and \(B\) of masses \(m_A\) and \(m_B\), respectively. Assume these two balls with different velocities, \(u_A\) and \(u_B\), are travelling in the same direction along a straight line. Note that no external unbalanced forces are acting on them.
Now, the two balls are colliding with each other, and let us say \(u_A\) \(>\) \(u_B\).
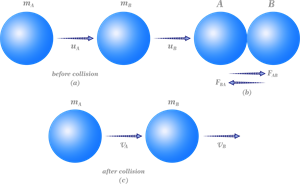
During the collision, ball \(A\) exerts a force \(F_{AB}\) on ball \(B\), and ball \(B\) exerts a force \(F_{BA}\) on ball \(A\) for time \(t\). After the collision, the two balls \(A\) and \(B\) have the velocities \(v_A\) and \(v_B\), respectively.
From, \(p\) \(=\) \(m v\),
Momenta of ball \(A\) before collision \(=\) \(m_A\) \(u_A\)
Momenta of ball \(A\) after collision \(=\) \(m_A\) \(v_A\)
Hence during the collision, the rate of change of momentum of ball \(A\),
Likewise, the rate of change of momentum of ball \(B\),
By the third law of motion, the force \(F_{AB}\) exerted by ball \(A\) on ball \(B\) is equal and opposite to the force \(F_{BA}\) exerted by ball \(B\) on ball \(A\).
On equating, we get
Total momentum of the two balls \(A\) and \(B\), before the collision \(=\) \(m_A\) \(u_A\) \(+\) \(m_B\) \(u_B\)
Total momentum of the two balls \(A\) and \(B\), after the collision \(=\) \(m_A\) \(v_A\) \(+\) \(m_B\) \(v_B\)
Important!
The total momentum of the two balls is conserved or unchanged without any action of external force.
Law of conservation of momentum
In the absence of unbalanced external force, the sum of momenta of the two objects before and after the collision will be equal. Or, the total momentum of the two objects is unchanged or conserved by the collision.
Conservation laws in physics
Conservation laws, such as conservation of momentum, energy, angular momentum, and charge, are considered fundamental. These are founded on tests, observations. Note that these conservation laws cannot be proven, but experiments may either suggest or disprove them. An experiment that yields a consistent result with the law verifies the law rather than proving it. A single experiment with a result that contradicts the law is sufficient to disprove it.
A significant number of findings and experiments have led to the discovery of the law of conservation of momentum. This law was formulated nearly three centuries ago, but no condition has arisen that violates this rule. This law of conservation of momentum describes a variety of everyday interactions or events.
