PDF chapter test TRY NOW
An object is said to be accelerating when its velocity changes. Any changes in the magnitude or direction of motion, or both, may cause the velocity to change. Sometimes, an object may not change its magnitude of velocity but only its direction of motion.
Case 1:
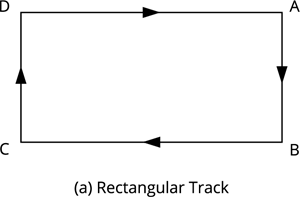
The image shows the path of an athlete along a rectangular track \(ABCD\). Imagine an athlete runs on the straight paths \(AB\), \(BC\), \(CD\) and \(DA\) of the rectangular track in uniform speed. Suddenly, he changes his running speed at the corners to keep himself on track.
Hence, to complete one round in a rectangular track, the athlete must change his direction of motion four times.
Case 2:
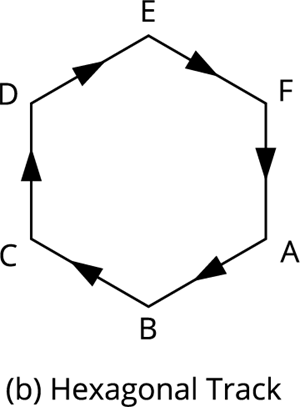
Now, imagine an athlete runs on the hexagonal shaped path \(ABCDEF\) instead of a rectangular track. For completing one round in a hexagonal track, the athlete must change his direction of motion six times.
Case 3:
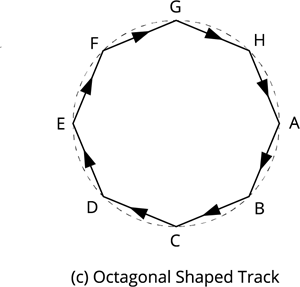
Again instead of a hexagonal shaped path, imagine the athlete runs on an octagonal path \(ABCDEFGH\). Then, the athlete has to take eight turns on each side to complete one round on the track.
From all these three cases, it is clearly evident that the athlete has to take more turns as the number of sides of the track increases.
Now, if the sides of the track keep on increasing, then the shape of the track changes to the shape of a circle, and the length of each side will decrease to a point.
Even if the athlete runs at constant magnitude along the circular path, the only difference in the velocity occurs due to the change in the direction of motion. As a result, the athlete's motion along a circular path is an example of accelerated motion.
Circumference of a circle of radius (\(r\))
If the athlete completes one round on the circular path of radius \(r\) in \(t\ seconds\), then the speed \(v\) is given as,
