PDF chapter test TRY NOW
Series connection of parallel resistors:
A series-parallel circuit is formed by connecting a set of parallel resistors in series.
- Connect \(R_1\) and \(R_2\) in parallel to obtain an effective resistance of \(R_{P1}\).
- Similarly, connect \(R_3\) and \(R_4\) in parallel to get an effective resistance of \(R_{P2}\).
- These parallel segments of resistors are then joined in series.
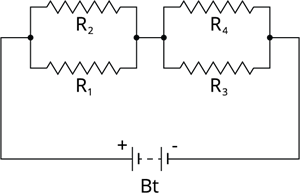
Series-parallel combination of resistors
The formula for the effective resistance of the parallel combination of resistors is
For two resistors in the circuit, the effective resistance is given as
Using the effective resistance of the series circuit, , the net effective resistance of the series-parallel combination of resistors is,
Parallel connection of series resistors:
A parallel-series circuit is formed by connecting a set of series resistors in parallel.
- Connect \(R_1\) and \(R_2\) in series to get an effective resistance of \(R_{S1}\).
- Similarly, connect \(R_3\) and \(R_4\) in series to get an effective resistance of \(R_{S2}\).
- These series segments of resistors are then joined in parallel.
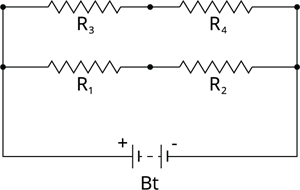
Parallel-series combination of resistors
Using the effective resistance of the series circuit, , we get
Using the formula for the effective resistance of the parallel combination of resistors , the net effective resistance of parallel-series combination of resistors is
.
