
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoA system of resistors is a combination or a group of resistors in a circuit.
The resistors can be connected in different combinations to form an electric circuit. But, there are only two basic methods of joining resistors. These are:
a) Resistors in series
b) Resistors in parallel
We can easily compute the effective resistance of resistors with different resistance values when it is connected in series and parallel.
Resistors connected in series:
In a series circuit, the electrical components are connected in a single loop, one after the other. The electric charge in a series circuit can only flow in one direction.
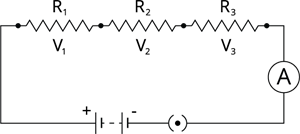
Series connection of resistors
If the circuit is broken or disturbed at any point in the loop, the current cannot flow through the circuit, and hence electric appliances linked to it will not function.
Let the resistances of three resistors be \(R_1\), \(R_2\) and \(R_3\), connected in series, and 'I' be the current flowing through the circuit. According to Ohm's law, the potential differences \(V_1\), \(V_2\) and \(V_3\) across \(R_1\), \(R_2\) and \(R_3\), respectively, are given by
The sum of the potential differences across the ends of each resistor is given by
Substituting the values of \(V_1\), \(V_2\) and \(V_3\) in the above equation, we get
---- (eq. 1)
A single resistor that can effectively replace all the resistors in the electric circuit to maintain the same current is known as an effective resistor.
Let \(R_S\) be the effective resistance of the series-combination of the resistors. Then, the (eq. 1) becomes
\(V\) \(=\) \(I\ R_S\)
\(\)
On substituting the values of effective resistance \(V\) in (eq. 1), we get
\(\)
\(\)
Important!
In a series circuit, the effective or equivalent resistance is equal to the sum of the individual resistances of the resistors.
When '\(n\)' number of resistors with an equal resistance '\(R\)' are connected in series, their equivalent resistance is given as '\(n R\)'. Hence,
\(R_S\) \(=\) \(n R\)
Important!
The equivalent resistance in a series combination is greater than the highest of the individual resistances.
From the diagram, it is deduced that the current '\(I\)' remains constant throughout the series circuit. In other words, the current in every point or junction of the circuit is the same.