PDF chapter test TRY NOW

22. Fundamental laws of gas - Charles's and Avogadro's law

Charles's Law:

Jacques Charles, a French scientist, formulated Charles's law in \(1787\). It is also known as the law of volume.

The statement of Charles's law is as follows:

The volume (\(V\)) of a given mass of a gas, at constant pressure (\(P\)), is directly proportional to its absolute temperature (\(T\)).

As a mathematical equation, Charles's law is written as either:

\begin{array}{l} V \propto T, or \\ VT = k_{2} \end{array}

Where,

\begin{array}{l} V - Volume of the gas \\ T - Temperature of the gas \\ K_{2} - Constant \end{array}

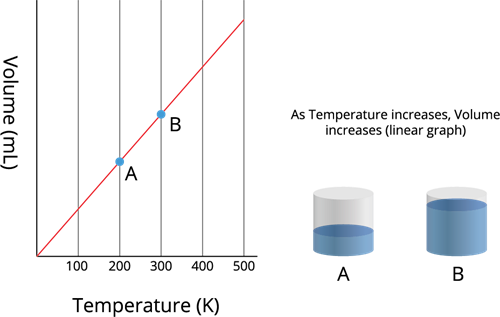
Charles's law - Temperature vs Volume

Another form of the equation (assuming there are two sets of conditions and setting both constants to each other) that might help solve problems is,

\frac{V_{1}}{T_{1}} = k_{2} = \frac{V_{2}}{T_{2}}

Where,

\begin{array}{l} V_{1} and V_{2} - Intial and Final volume of the gas \\ T_{1} and T_{2} - Intial and Final temperature of the gas \\ K_{2} - Constant \end{array}

Avogadro's law:

Amedeo Avogadro proposed Avogadro's law in \(1811\).

The statement of Avogadro's law is as follows:

It states that the volume occupied by an ideal gas is directly proportional to the number of atoms or molecules of the gas present in the container at constant pressure and temperature.

As a mathematical equation, Avogadro's law is written as either:

\begin{array}{l} V \propto n, or \\ Vn = z \end{array}

Where,

\begin{array}{l} V - Volume of the gas \\ n - No . of atoms or molecules of the gas \\ z - Constant \end{array}

Molecular addition

Another form of the equation (assuming there are two sets of conditions and setting both constants to each other) that might help solve problems is,

\frac{V_{1}}{n_{1}} = z = \frac{V_{2}}{n_{2}}

Where,

\begin{array}{l} V_{1} and V_{2} - Initial and Final volume of the gas \\ n_{1} and n_{2} - Initial and Final amount (atoms or molecules) of the gas \\ z - Constant \end{array}

Previous theory

Exit to the topic

Next theory

Send feedback

Did you find an error?

Send it to us!

22. Fundamental laws of gas - Charles's and Avogadro's law

Theory: