PDF chapter test TRY NOW

Linear expansion in solid
The increase in the length is proportional to the rise in temperature, original length, and material type.
The amount by which the unit length of a material increases when the temperature is raised one degree is called the coefficient of linear expansion. The unit of coefficient of linear expansion is . The value of the coefficient of linear expansion is different for different materials.
The coefficient of linear expansion is used to find out the actual increase in the length. It can be represented by the symbol (alpha).
Consider a material with the length of at \(c\). The material is heated up to \(c\). Now, the length of the material is .
Let be the coefficient of linear expansion.
We know that,
The change in length \(ΔL\) is proportional to the original length , rise in temperature \(ΔT\), and material type.
Rearranging the above equation,
---- eqn 1
The will vary for different materials.
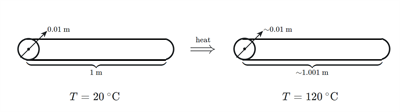
In above diagram,
= \(1\) \(m\)
= \(c\)
= \(c\)
= \(1.001\) \(m\)
then,
= \(0.0000099\).
We shall calculate the length after the expansion using the equation.
Change (increase) in length,
:
