
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoFrom the early \(17th\) century, the gas laws have been around to help scientists find the amount of gas, volumes, pressures, and temperature when coming to gas matters.
The gas laws consist of three primary laws:
- Charles' Law
- Boyle's Law and
- Avogadro's Law
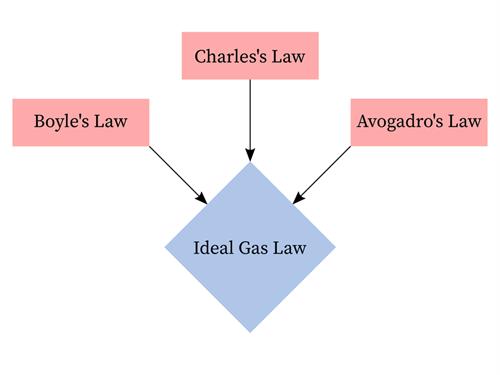
Fundamental gas laws
The three fundamental gas laws are used to find the relationship between pressure, temperature, volume, and the amount of gas.
- Boyle's law describes that the volume of gas increases as the pressure decreases.
- Charles' law states that the volume of gas increases as the temperature increases.
- Avogadro's law says that the volume of gas increases as the amount of gas increases.
The ideal gas law is the combination of the three simple gas laws.
Boyle's Law:
In 1662, Robert Boyle investigated the relationship between volume and pressure of a gas of a fixed amount at a constant temperature. He found that the volume of a given mass of a gas is inversely proportional to its pressure at a constant temperature.
A statement of Boyle's law is as follows:
When the temperature of a gas is kept constant, the volume of a fixed mass of gas is inversely proportional to its pressure.
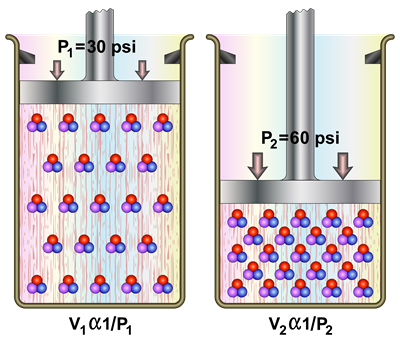
Relation between pressure and volume
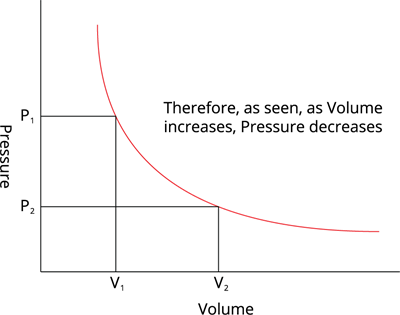
Volume vs Pressure, at constant temeperature
In other words, at a constant temperature, the product of the pressure and volume of a given mass of an ideal gas in a closed system is always constant.
Where,
P - Pressure
V - Volume occupied by a gas
k - Constant
Boyle’s Law can be used to determine the current pressure or volume of gas and can be represented also as,
Where,