
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoLength is one of the fundamental quantity that cannot be conveyed in any other way. Other measurements, such as area and volume, can be calculated using length.
Area
In general, two lengths are used to calculate the area of an object.

The formula is given as,
By using the above formula, the area of a book, house or even a garden can be found. The SI unit for the area of a surface is \(m^2\) since it is a product of two lengths.
Example:
Assume the length and breadth of the wall are \(20\ m\) and \(8\ m\), respectively. Then, what will be the area of the wall?

Length of the wall \(=\) \(20\ m\)
Breadth of the wall \(=\) \(8\ m\)
Therefore, the area of the wall is \(160\) \(m^2\).
Volume of solids
A volume is the amount of space occupied by any three-dimensional object. It is also a derived quantity that can be measured by measuring lengths. The formula is written as,
The SI unit of volume is a \(cubic\) \(metre\) or \(m^3\).
Calculation of volume of a solid box
A volume of a solid box can be found using three parameters such as length (\(l\)), breadth (\(b\)) and height (\(h\)). These parameters are measured using a measuring scale in terms of \(cm\) or \(m\).
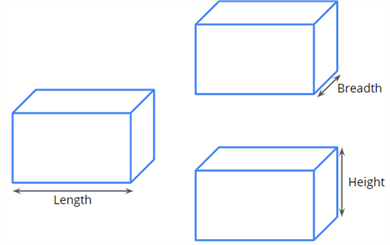
If the unit of volume is written in \(cm\), then
\(Volume\) \(=\) \(centimetre\) \(×\) \(centimetre\) \(×\) \(centimetre\)
\(=\) \(cubic\ centimetre\) or \(cm^3\)
Example:
Look at the image of the solid box and calculate its volume.

The dimensions of the solid box are given below:
Length, \(l\ = 10\ cm\)
Breadth, \(b\ = 10\ cm\)
Height, \(h\ = 10\ cm\)
Length, \(l\ = 10\ cm\)
Breadth, \(b\ = 10\ cm\)
Height, \(h\ = 10\ cm\)
By substituting the known value on the formula, we get the following.
If the volume of a solid cubical box is \(1000\ cubic\ cm\), then it means that \(1000\) cubes, each with dimensions \(1 cm\) \(×\) \(1 cm\) \(×\) \(1 cm\), can be placed inside the box.