PDF chapter test TRY NOW
Volume is a space occupied by any three-dimensional object. It is also a derived quantity that can be measured by measuring lengths.
The formula is written as,
SI Unit
If the unit of volume is written in \(m\), then
\(Volume\) \(=\) \(metre\) \(×\) \(metre\) \(×\) \(metre\)
\(=\) \(cubic\ metre\) or \(m^3\)
Hence, the SI unit of volume is a \(cubic\) \(metre\) (or) \(m^3\).
The volume of regularly shaped objects
The volume of regularly shaped figures can be calculated using the relevant formula. Some of them are tabulated below.
Shape | Three-dimensional figure | Volume |
Cube |  | |
Cuboid | 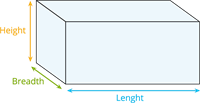 | |
Sphere |  | |
Cylinder | 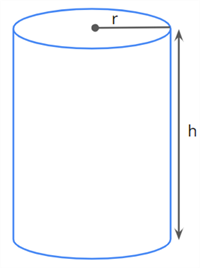 |
Solved examples
1. Calculate the volume of a cube having sides of \(10\ m\).
Sides, \(a\ = 10\ m\)
Sides, \(a\ = 10\ m\)
By substituting the known values on the formula of a cube, we get the following.
Therefore, the volume of a cube is \(1000\ m^3\).
2. What will be the volume of a cylinder having a \(2\ m\) radius and \(7\ cm\) height?
Radius, \(r\ = 2\ m\)
Height, \(h\ = 7\ m\)
Therefore, the volume of a cylinder is \(1000\ cm^3\).
Reference:
https://upload.wikimedia.org/wikipedia/commons/d/df/Simple_sphere_with_radii.svg
