
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoIntroduction to Carbon:
Carbon is one of the fundamental non-metallic element. Antoine Lavoisier named carbon from the Latin word ‘Carbo’, meaning coal. Carbon is the main component of coal. Coal is a fossil fuel developed from the prolonged decomposition of buried plants and animals. So, it is clear that all life forms include carbon.

Coal mining
The earth's crust includes only \(0.032%\) carbon (\(320\) ppm by weight) in the form of carbonates, gas and petroleum, while the atmosphere contains only \(0.03%\) carbon dioxide (i.e.\(300\) ppm by weight). As a result, even though carbon compounds are found in limited quantities in nature, they are essential in our daily life.
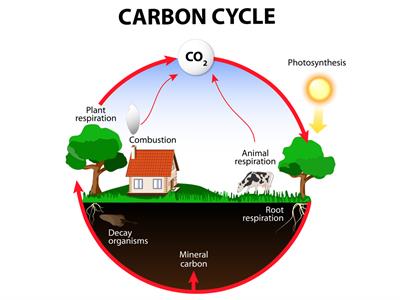
Carbon can be found in our muscles, bones, organs, blood and other components of living thins. A vast number of products that we use in our daily life are made up of carbon compounds. So, without carbon, there is no possibility of plants and animals, including humans. Thus, Carbon Chemistry is also called Living Chemistry. In this lesson we will study the unique features of carbon, its properties, and plastic, which is a catenated long-chain compound.
Discovery of Carbon Milestones:

Different forms of carbon
Carbon has been known since early times in the form of soot, charcoal, graphite and diamonds. However, ancient cultures did not realise that these substances were different forms of the same element.
In \(1772\), French scientist Antoine Lavoisier along with other chemists, bought a diamond and experimented by placing it in a closed glass jar. They directed the Sun’s rays on the diamond with a special giant magnifying glass and saw the diamond burn and disappear.

Antoine Lavoisier
Lavoisier saw that the overall weight of the jar was unchanged and that when it fired, the diamond had reacted with oxygen to form carbon dioxide. Thus, he decided that diamond and charcoal were made of the same element - Carbon.

Charcoal and diamond
In \(1779\), Swedish expert Carl Scheele noted that graphite also burned to form carbon dioxide. In \(1796\), English chemist Smithson Tennant discovered that diamond is pure carbon and not a carbon compound, and it burned to produce only carbon dioxide. Tennant also proved that when the same weights of charcoal and diamonds were burned, they produced the same carbon dioxide.

Diamond
In \(1855\), English chemist Benjamin Brodie produced pure graphite from carbon, proving graphite is a form of carbon. Although this experiment was previously attempted without success, in \(1955\), American scientist Francis Bundy and his co-workers at General Electric company finally demonstrated that graphite could be transformed into diamond under high temperature and pressure.
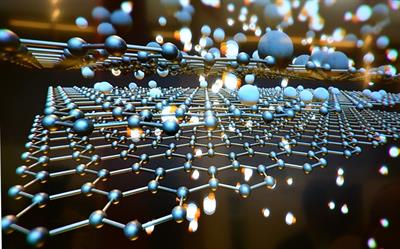
Graphene hexagonal arrangement of carbon
In \(1985\), Robert Curl, Harry Kroto and Richard Smalley found fullerenes, a new type of carbon in which the atoms are organised in soccer-ball shapes. Graphene consists of a single layer of carbon atoms arranged in hexagons. Graphene discovery was declared in \(2004\) by Kostya Novoselov and Andre Geim, who used adhesive tape to divide a single layer of atoms from graphite to create the new allotrope. If these layers were stacked upon one other, graphite would be the result. As a result, graphene has a thickness of just one atom.