
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoIf a current \(I\) flows through a conductor of length \(L\), that is kept perpendicular to the magnetic field \(B\), the force \(F\) that it experiences is given by the equation,
According to the above equation, the force is proportional to the current through the conductor, the length of the conductor, and the magnetic field in which the current-carrying conductor is kept.
The magnetic force is also affected by the angle of inclination between the current and magnetic field. The force is huge when the conductor is perpendicular to the magnetic field (=BIL). The force is zero when it is parallel to the magnetic field.
Force is a vector quantity as it has both magnitude and direction. It implies that we should be aware of the force's direction of action. Fleming's Left-hand rule is frequently used to determine the direction (formulated by scientist John Ambrose Fleming).
Fleming's Left-Hand rule:
According to the law, stretch the three fingers of the left-hand perpendicular to each other, the middle finger denotes the direction of the current and the second finger denotes the direction of the magnetic field, then the thumb of the left hand indicates the direction of the force or movement of the conductor.
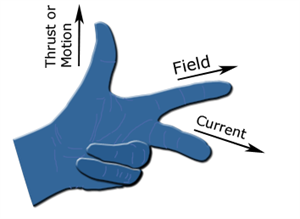
Picture depicting Fleming's left-hand rule
Example:
A conductor, which has a length of 40 \(cm\) that carries a current of 10 \(A\), is placed perpendicular to a magnetic field of induction \(T\). Find the force on the conductor.
Solution:
Length of the conductor(\(L\)) \(=\) 40 \(cm\) \(=\) \(m\)
Current flowing through the conductor (\(I\)) \(=\) 10 \(A\)
Magnetic field of induction(\(B\)) \(=\) \(T\)
To find: Force on the conductor
Reference:
https://commons.wikimedia.org/wiki/File:LeftHandOutline.png