PDF chapter test TRY NOW
Length can be defined as the difference between the two points.
For example, if you want to measure your body length (height), you should find the length between your head and your toe.

Measuring length
The SI unit of length is a metre. One metre is the distance travelled by light through vacuum in \(1/29,97,92,458\) \(second\).
Similarly, we use this fundamental quantity to measure the distance also. Usually, we calculate the distance in centimetres or metres. But if the distance is huge, we use Kilometre.
Have you ever wondered how we calculate the distance at sea?
We use the term nautical miles to measure the distance at sea.
\(1\) mile \(=\) \(1.6\) Kilometres.
\(1\) nautical mile \(= 1.852\) Kilometres at sea.
Now, we know how to calculate the distance at sea. But, How do you calculate the distance in space?
To measure the very large and enormous distance, we use the following units.
1. Light years
2. Astronomical units and
3. Parsec
1. Light years:
Knowing that light travels per second.
A light-year is a distance travelled by light in one year in a vacuum, and it is equal to m or
\(1\) Light year:
To calculate one light-year, multiply the total number of days in a year, hours in a day, minutes and seconds, and the product of this value should be multiplied by
\(1\) Light year \(= (365 × 24 ×60 × 60) ×( 3×10^8) \)
\(1\) Light year \(=\) 31536000 \(×( 3×10^8) \)
\(1\) Light year \(=\) 9460800000000000 \(= 9.46×10^15\)m
2. Astronomical units:
Astronomical units are used to calculate the distance between the Sun and the Earth.
It is the mean distance of the centre of the Sun from the centre of the earth.
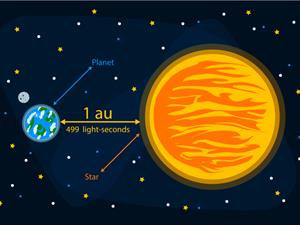
Astronomical unit
3. Parsec:
Parsec is the unit of distance. We can use this method to measure astronomical objects outside the solar system.
Important!
The nearest star, Alpha Centauri, is about \(1.34\) \(parsec\) from the sun. Most of the stars visible to the unaided eye in the night sky are within \(500\) \(parsec\) distance from the sun.
Note:
Larger units | In metre |
Kilometre (km) | |
Astronomical unit (Au) | |
Light year (ly) | |
Parsec (pc) |
To measure small distances such as distance between two atoms in a molecule, size of the nucleus and wavelength etc.,. we use submultiples of ten. These quantities are measured in Angstrom unit.
Smaller units | In metre |
Fermi (f)* | |
Angstrom (A)* | |
Nanometre (nm) | |
Micron (micrometre ) | |
Millimetre (mm) | |
Centimetre (cm) |
* Unit outside SI system and still accepted for use.
