
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoNewton observed that the motion of an object gives a set of three equations of motion which relate to the displacement, velocity, acceleration and time of an object under motion, and, these equations are called as the equation of motion.
Now, let us learn about the equations of motion.
Equations of motion:
Equations of motion are equations that describe behaviour of a physical system in terms of its motion as a function of time.
More specifically, the equations of motion describe the behaviour of a physical system as a set of mathematical functions in terms of dynamic variables.
The variable include a displacement, velocity, acceleration and time of an object under motion. An object is in motion with initial velocity (u) attains a final velocity (v) in time (t) due to acceleration (a), with displacement (s). The three equations of motion can be written as,
The three equations are:
1.
2.
3.
These equations apply to a particle or an object moving linearly, in three dimensions in a straight line with constant acceleration. Because, the motion is along a straight line, the problem effectively reduces from three dimensions to one as plotted in the graph.
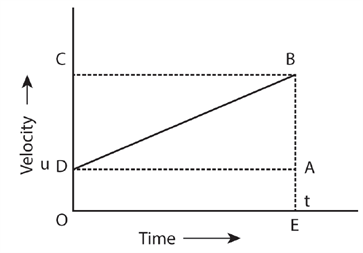
From the above graph, we can observe that the velocity changes with time for a uniformly accelerated object.
The object starts from the point \(D\) in the graph with velocity \(u\). The velocity of an object keeps increasing, and after time \((t)\), it reaches the point \(B\) on the graph.
Therefore, the initial velocity of the object \(u =\) \(OD = EA.\)
Then, the final velocity of an object \(v =\) \(OE = DA.\)
Time \(= t = OE = DA\)
From the graph, we can also find that \(AB = DC.\)
i) First equation of motion:
We already knew that acceleration \(a\) is = Change in velocity \(/\) time.
Change in velocity can be defined as final velocity \(-\) Initial velocity.
Therefore,
Hence \(t = OE\), we can simplify the equation as,
From the graph, \(EB = EA + AB\), if we substitute the known values, we get,
\(EB = v \),
\(EA = u \),
\(AB = at\).
, this is the first equation of motion.
ii) Second equation of motion:
From the graph, the distance covered by object during time \(t\) is given by the area of quadrangle \(DOEB\),
Therefore, \(s =\) The area of the quadrangle \(DOEB =\) Area of the rectangle \(DOEA\) \(+\) Area of the triangle \(DAB\)
Substitute the known values, then we get,
This is second equation of motion.
iii) Third equation of motion:
From the graph, the distance covered by the object during time t is given by the area of the quadrangle \(DOEB\). Here \(DOEB\) is a trapezium.
Then, \(S =\) The area of trapezium \(DOEB = 1/2 ×\) sum of the length of parallel side \(×\) distance between parallel sides.
This is the third equation of motion.
In the next exercise, we will see the application of these equations.
Reference:
Reference:
Tamilnadu text book 9th standard science term -I page no. 27 - https://drive.google.com/file/d/1DK3TZfkuReocATyB0V-tA1U5B7eRws2A/view