
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoமுந்தைய பகுதிகளில், விசையின் திருப்புத்திறன்பற்றி படித்தோம்.
இந்தப் பகுதியில், நேர்க்கோட்டு உந்த அழிவின்மை விதி பற்றி அறிந்துகொள்வோம் மற்றும் அவற்றை ஒரு எடுத்துக்காட்டுடன் நிரூபிப்போம்.
நேர்க்கோட்டு உந்த அழிவின்மை விதி:
புற விசை எதுவும் செயல்படாத வரையில் ஒரு பொருள் அல்லது ஓர் அமைப்பின் மீது செயல்படும் மொத்த நேர்க்கோட்டு உந்தம் மாறாமல் இருக்கும்.
கீழ் கண்ட ஒரு எடுத்துக்காட்டின் மூலம் நேர்க்கோட்டு உந்த அழிவின்மை விதியினை நிரூபிக்கலாம்:
\(A\) மற்றும் \(B\) என்ற இருபொருட்களை எடுத்து கொள்வோம்.
அவைகளின் நிறைகள் முறையே \(m_1\) மற்றும் \(m_2\) என்க.
அவை \(u_1\) மற்றும் \(u_2\) ஆரம்ப திசை வேகத்தோடு நேர்க்கோட்டில் பயணிப்பதாக கொள்வோம்.
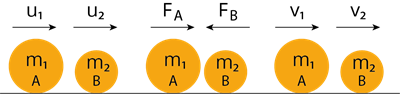
நேர்க்கோட்டு உந்த அழிவின்மை விதியினை நிரூபித்தல்
பொருள் \(A\) னது,\( B\) ஐ விட அதிக திசைவேகத்தில் செல்வதாக கருதுவோம் (\(u_1\ >\ u_2\)). பொருள் \(A\) னது, \(B\) யுடன் ‘\(t\)’ என்ற கால இடைவெளியில் மோதலை ஏற்படுத்துகிறது.
அப்பொருள்கள் மோதலுக்குப் பிறகு அதே நேர்க்கோட்டில் \(v_1\) மற்றும் \(v_2\) திசைவேகத்தில் பயணிப்பதாக கொள்வோம்.
நியூட்டனின் இரண்டாம் விதிப்படி,
\(B\) யின் மீது \(A\) செயல்படுத்தும் விசை \(FA\) \(=\) \(\frac{m_2 \times (v_2\ -\ u_2)}{t}\)
அதேபோல்
\(A\) யின் மீது \(B\) செயல்படுத்தும் விசை \(F_B\ =\ \frac{m_1 \times (v_1\ –\ u_1)}{t}\)
\(A\) யின் மீது \(B\) செயல்படுத்தும் விசை \(F_B\ =\ \frac{m_1 \times (v_1\ –\ u_1)}{t}\)
நியூட்டனின் மூன்றாம் விதிப்படி \(A\)ன் மீது செயல்படும் விசையானது \(B\)ன் மீது செயல்படும் எதிர்விசைக்கு சமம்
\(\text{விசை}\ =\ \text{எதிர்விசை}\)
\(F_B\ =\ –F_A\)
\(\frac{m_1 \times (v_1\ –\ u_1)}{t}\) \(=\ –\)\(\frac{m_2 \times (v_2\ -\ u_2)}{t}\)
\(m_1 \times v_1\ -\ m_1 \times u_1\ =\ -m_2 \times v_2\ +\ m_2 \times u_2\)
\(m_1 \times v_1\ +\ m_2 \times v_2\ =\ m_1 \times u_1\ +\ m_2 \times u_2\)
மேற்காண் சமன்பாடு, இந்நிகழ்வில் வெளிவிசையின் தாக்கம் எதும் இல்லாதபோது, மோதலுக்கு பின் உள்ள மொத்த உந்த மதிப்பு, மோதலுக்கு முன் உள்ள மொத்த உந்த மதிப்பிற்கு சமம் என்பதை காட்டுகிறது.
இது பொருளின் மீது செயல்படும் மொத்த உந்தம் ஒரு மாறிலி என்ற நேர்க்கோட்டு உந்த அழிவின்மை விதியினை நிரூபிக்கிறது