PDF chapter test TRY NOW
சரிவகத்தின் பரப்பளவைக் கணக்கிட, இணையான பக்கங்களின் கூட்டுத்தொகையை அவற்றுக்கிடையே செங்குத்தாகப் பெருக்கி 2 ஆல் வகுக்க வேண்டும்.
சரிவகத்தின் பரப்பளவு A = (a + b)×h சதுர அலகுகள்
A என்பது சரிவகத்தின் பரப்பளவு.
'a' மற்றும் 'b' என்பது இணையான பக்கங்களின் நீளம்.
'h' என்பது இணையான பக்கங்களுக்கு இடையே உள்ள செங்குத்தாக இருக்கும் தூரம்.
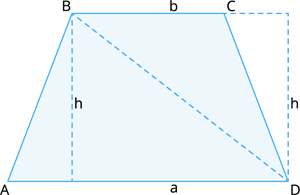
சரிவகத்தை இரண்டு முக்கோணங்களாகப் பிரிப்பதன் மூலம் சரிவகத்தின் பரப்பளவிற்கான சூத்திரத்தைப் பெறுவோம்.
பரப்பளவு A = (a + b)×h சதுர அலகுகளின் பரப்பளவை நிரூபிக்க.
சாிவகத்தின் பரப்பளவு ABCD = Δ ABDன் பரப்பு + ΔCBDன் பரப்பு.
இப்போது, ΔABD மற்றும் ΔBCDயின் பரப்பளவைத் தனித்தனியாகக் கண்டறிந்து, சரிவகத்தின் பரப்பைப் பெற அவற்றைச் சேர்க்கவும்.
ΔABDன் பகுதி + ΔCBD ன் பகுதி = b × h + b × h.
மேலே உள்ள படத்தில் இருந்து, ΔABD = a ன் அடிப்பகுதி மற்றும் ΔCBD = b ன் அடிப்பகுதி
மேலும், முக்கோணங்களின் உயரம், ΔABD = ΔCBD = h.
அறியப்பட்ட மதிப்பை உள்ளிடவும்.
சாிவகத்தின் பரப்பளவு ABCD = b × h + a × h.
பொதுவாக h எடுத்துக் கொள்வோம்:
= (a + b)× h
இவ்வாறு, சாிவகத்தின் பரப்பளவு ABCD = (a + b)×h சதுர அலகுகள்.
Register for free to see more content