
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoஇயற்கணிதக் கோவை:
கோட்பாடு: ஒரு இயற்கணிதக் கோவை என்பது மாறிலிகள், மாறிகள் மற்றும் அதை இணைக்கும் இயற்கணித செயல்பாடுகள் சேர்ந்த ஒரு வடிவமே.
உறுப்புகள் மற்றும் காரணிகள்:
கோட்பாடு: ஒரு இயற்கணிதக் கோவையில் அமைந்துள்ள ஒவ்வொரு எண்ணும், எழுத்தும் அந்தக் கோவையின் காரணிகள் ஆகும்.
காரணிகள் தனித்தோ, இணைந்தோ வந்து உறுப்புகளை உருவாக்கும். இவற்றை பிணைக்கும் கருவியாக அடிப்படைக் கணித செயலிகள் அமையும்.
காரணிகள் தனித்தோ, இணைந்தோ வந்து உறுப்புகளை உருவாக்கும். இவற்றை பிணைக்கும் கருவியாக அடிப்படைக் கணித செயலிகள் அமையும்.
உதாரணமாக:
\(5a − 3\) இந்த இயற்கணிதக் கோவையில் , \(5a\) என்பது முதல் உறுப்பு. \(3\) என்பது இரண்டாவது உறுப்பு.
எனவே, இதில் \(2\) உறுப்புகள் உள்ளன.
எனவே, இதில் \(2\) உறுப்புகள் உள்ளன.
இதில் \(3\) என்பது தனித்து உள்ளது. \(5a\) என்ற உறுப்பில் \(5\) மற்றும் \(a\) என்கிற இரண்டு காரணிகள் உள்ளன. இதில் \(5a\) என்பது \(5\) மடங்கு \(a\).
கோட்பாடு:
கலப்பு உறுப்புகள் ஒரு எண்ணின் அல்லது எழுத்தின் பெருகற்பலனாக அமைகிறது. ஒன்றன் மடங்குகளாக நிற்கிறது. ஒரு உறுப்பில் உள்ள ஒரு காரணிக்கு மற்ற காரணிகள் கெழுவாக அமையும்.
கெழு எண்ணாக இருந்தால் அது எண் கெழு என்றழைக்கப்படும்.
இங்கு, \(5\) என்பது எண் கெழு;
\(a\) என்பது மாறி;
\(3\) என்பது மாறிலி.
\(a\) என்பது மாறி;
\(3\) என்பது மாறிலி.
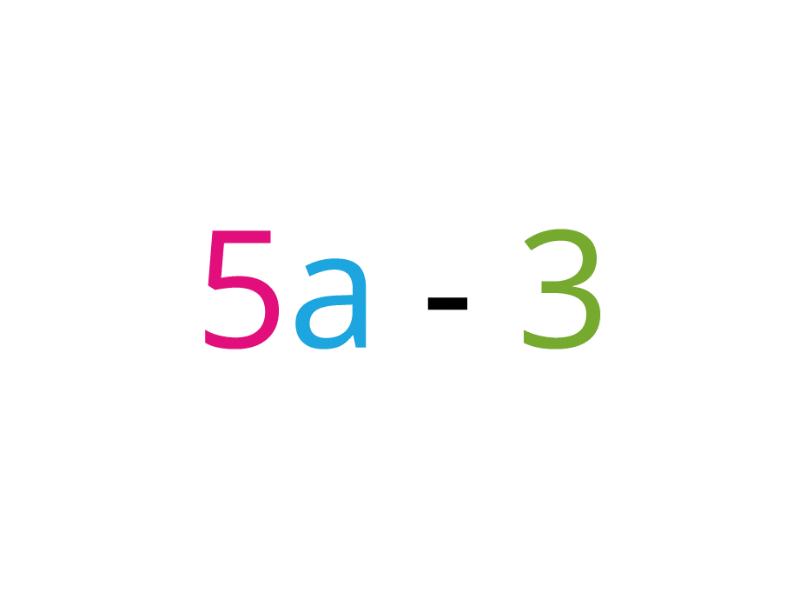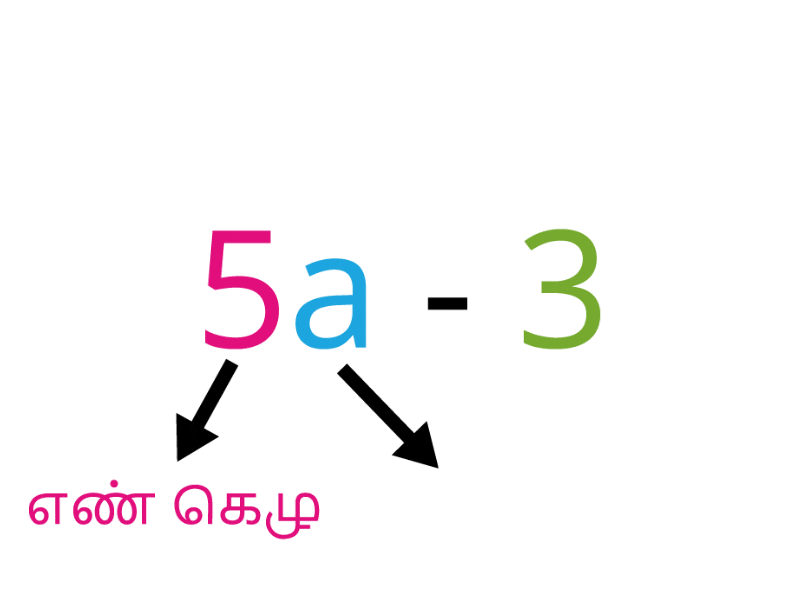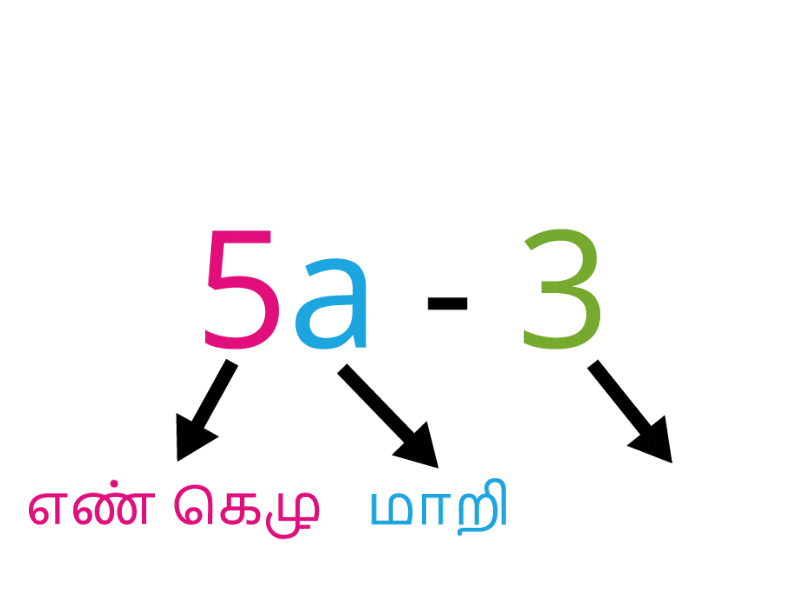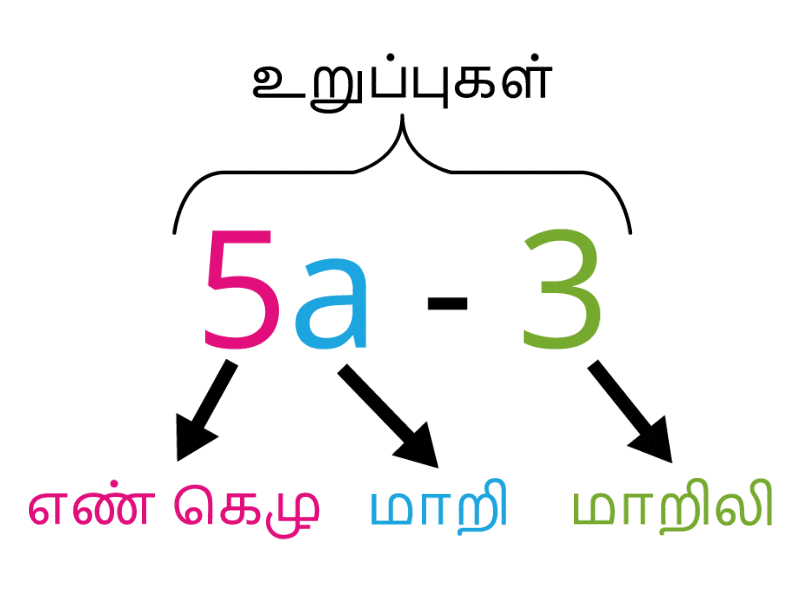
உதாரணமாக:
பின்வரும் இயற்கணிதக் கோவையில் உறுப்புகளையும், கெழுக்களையும் பட்டியலிடுங்கள்:
\(4x^3y^2+2x^2-3x+4\).
உறுப்புகள்:
- \(4x^3y^2\) என்பது முதல் உறுப்பு.
- \(2x^2\) என்பது இரண்டாவது உறுப்பு.
- \(-3x\) என்பது மூன்றாவது உறுப்பு.
- \(4\) என்பது நான்காவது உறுப்பு.
கெழுக்கள்:
- \(4\) என்பது \(x^3y^2\)ன் எண் கெழுவாகும்.
- \(2\) என்பது \(x^2\)ன் எண் கெழுவாகும்.
- \(-3\) என்பது \(x\)ன் எண் எழுவாகும்
\(4x^3y^2\) ஐ எடுத்துக்கொள்வோம். இதில்;\(x^3\) இன் கெழு \(4y^2\)
- \(4\) இன் கெழு \(x^3y^2\)
- \(y^2\) இன் கெழு \(4x^3\)