PDF chapter test TRY NOW
ஒரு நேர்க்கோட்டுச் சமன்பாடு இரண்டு மாறிகளில் அமைந்த சமன்பாடு எனில், அந்த வரைபடம் ஒரு
நேர்க்கோட்டைக் குறிக்கும்.
இரு மாறியில் அமைந்த வரைபடத்தை எடுத்துக்காட்டுடன் காணலாம்.
Example:
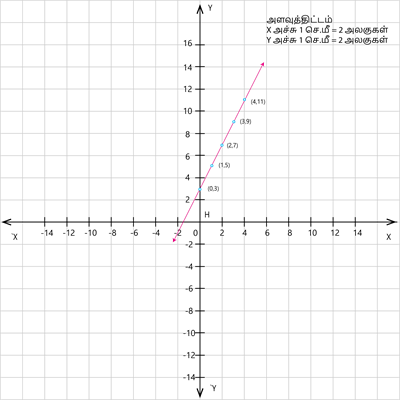
1. \(y = 2x + 3\) என்ற சமன்பாட்டிற்கு வரைபடம் வரைக.
தீர்வு:
\(x\) க்கு மதிப்புகள் கொடுக்கும்போது கீழ்க்கண்டவாறு \(y\) இன் மதிப்பு கிடைக்கும்.
\(x = 0\) எனும்போது, \(y = 2(0) + 3\) \(= 3\).
\(x = 1\) எனும்போது, \(y = 2(1) + 3\) \(= 5\).
\(x = 2\) எனும்போது , \(y = 2(2) + 3\) \(= 7\).
\(x = 3\)எனும்போது, \(y = 2(3) + 3\) \(= 9\).
\(x = 4\) எனும்போது, \(y = 2(4) + 3\) \(= 11\).
கிடைக்கப்பெற்ற மதிப்புகளை அட்டவணைப்படுத்தக் கிடைப்பது,
| \(x\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) |
| \(y\) | \(3\) | \(5\) | \(7\) | \(9\) | \(11\) |
எனவே, கிடைக்கப்பெற்ற புள்ளிகளை வரைபடத்தில் குறித்து கீழ்க்கண்டவாறு இணைக்கவும்.
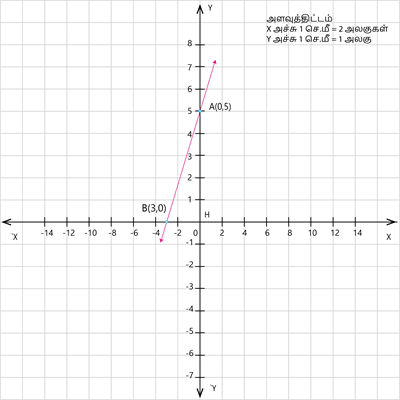
2. \(y = \frac{5}{3}x + 5\) என்ற சமன்பாட்டிற்கு வரைபடம் வரைக.
தீர்வு:
\(x\) க்கு மதிப்புகள் கொடுக்கும்போது கீழ்க்கண்டவாறு \(y\) இன் மதிப்பு கிடைக்கும்.
விகித எண்களின் விடையை தவிர்த்து முழுக்களை எடுத்துக்கொள்வதன் மூலம் எளிதாக வரைபடம் வரையலாம்.
\(x = 0\) எனும்போது,
\(y = \frac{5}{3}(0) + 5\)
\(y = 5\)
\(y = 0\) எனும்போது,
\(0 = \frac{5}{3}x + 5\)
\(-5 = \frac{5}{3}x\)
\(-5 \times \frac{3}{5} = x\)
\(-3 = x\)
எனவே, \((0,5)\) மற்றும் \((-3,0)\) என்ற புள்ளிகளை வரைபடத்தில் குறித்து கீழ்க்கண்டவாறு நேர்க்கோடு வரையலாம்.
வரைபடத்தின் பயன்பாடு
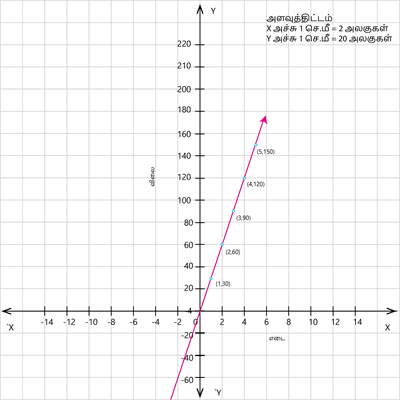
\(1\) \(\text{கி.கி}\) தக்காளியின் விலை \(₹30\) எனில் \(4.5\) \(\text{கி.கி}\) தக்காளியின் விலையை வரைபடம் மூலம் கண்டறிக.
தீர்வு:
கொடுக்கப்பட்டது: \(1\) \(\text{கி.கி}\) தக்காளி \(=₹30\).
எனவே,
\(2\) \(\text{கி.கி}\) \(= 2 \times 30\) \(= ₹60\).
\(3\) \(\text{கி.கி}\) \(= 3 \times 30\) \(= ₹90\).
\(4\) \(\text{கி.கி}\) \(= 4 \times 30\) \(= ₹120\).
\(5\) \(\text{கி.கி}\) \(= 5 \times 30\) \(= ₹150\).
கிடைக்கப்பெற்ற மதிப்புகளைக் கீழ்க்கண்ட படிகளின் மூலம் வரைபடத்தில் வரையலாம்.
படி \(1\): தக்காளியின் எடையை \(x\) அச்சில் எடுத்துக்கொள்வோம்.
படி \(2\): தக்காளியின் விலையை \(y\) அச்சில் எடுத்துக்கொள்வோம்.
படி \(3\): \((1,30)\), \((2,60)\), \((3,90)\), \((4,120)\) மற்றும் \((5,150)\) என்ற புள்ளிகளை வரைபடத்தில் குறிக்கவும்.
படி \(4\): புள்ளிகளை இணைக்கவும்
படி \(5\): வரைபடத்தின் மூலம், \(4.5 \)கி.கி தக்காளியின் விலை \(₹135\).
Register for free to see more content