PDF chapter test TRY NOW
தேற்றத்தின் கூற்று:
ஒரு செங்கோண முக்கோணத்தில் கர்ணத்தின் மீதமைந்த சதுரத்தின் பரப்பளவானது, மற்ற இரண்டு பக்கங்களின் மீதமைந்த சதுரங்களின் பரப்பளவுகளின் கூடுதலுக்குச் சமமாகும்.
செங்கோண முக்கோணம் \(ABC\) இல், \(AC^2=AB^2+BC^2\).
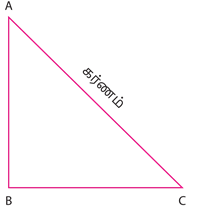
கொடுக்கப்பட்டது:
\(ABC\) என்பது ஒரு செங்கோண முக்கோணம்.
அதாவது, \(\angle ABC\) \(=\) \(90^{\circ}\).
நிரூபிக்க வேண்டியது:
\(AC^2=AB^2+BC^2\)
நிரூபணம்:
\(B\) லிருந்து \(AC\) க்கு \(BD \perp AC\) என்றவாறு \(BD\) என்ற நேர்க்கோடு வரைக.

\(ABC\) மற்றும் \(BDC\) என்ற முக்கோணங்களை எடுத்துக்கொள்வோம்.
\(\angle C\) என்பது இரண்டு முக்கோணங்களுக்கும் பொதுவான கோணம் ஆகும்.
இங்கு, \(BD \perp AC\).
எனவே, \(\angle BDC\) \(=\) \(90^{\circ}\).
மேலும், \(\angle ABC\) \(=\) \(90^{\circ}\).
கோ-கோ வடிவொத்தப் பண்பின்படி,(ஒரு முக்கோணத்தின் இரண்டு கோணங்கள், மற்றொரு
முக்கோணத்தின் இரண்டு கோணங்களுக்குச் சமம் எனில், அவ்விரு
முக்கோணங்களும் வடிவொத்தவை ஆகும்.) \(ABD\) மற்றும் \(BDC\) ஆகிய முக்கோணங்கள் வடிவொத்தவை.
எனவே, முக்கோணங்களின் பக்கங்களின் விகிதம் சமம் ஆகும்.
அதாவது, \(\frac{BC}{CD} = \frac{AC}{BC}\).
இதன் மூலம், \(BC^{2} = AC \times CD\) ……\((1)\)
தற்பொழுது, \(ABC\) மற்றும் \(ABD\) என்ற முக்கோணங்களை எடுத்துக்கொள்வோம.
மீண்டும் கோ-கோ பண்பின்படி, \(\frac{AB}{AD} = \frac{AC}{AB}\).
இதன் மூலம், \(AB^{2} = AC \times AD\) ……\((2)\)
\((1)\) மற்றும் \((2)\) வது சமன்பாட்டை கூட்ட,
\(BC^2 + AB^2\) \(=\) \((AC \times CD) + (AC \times AD)\)
\(=\) \(AC (CD +AD)\)
\(=\) \(AC \cdot AC\)
\(=\) \(AC^2\).
எனவே, \(AC^2 = AB^2 + BC^2\).
பிதாகரஸ் தேற்றம் நீருபிக்கப்பட்டது.
Example:
ஒரு செங்கோண முக்கோணத்தில் கர்ணம் \(29\) செ.மீ ஒரு பக்கம் \(21\) செ.மீ எனில் மற்றொரு பக்கத்தின் நீளம் காண்க:
தீர்வு:
\(ABC\) என்பது ஒரு செங்கோண முக்கோணத்தை படத்தில் காட்டியவாறு எடுத்துக்கொள்வோம்.
இங்கு, \(AC\) என்பது கர்ணம் ஆகும்.
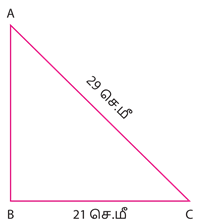
பிதாகரஸ் தேற்றத்தின்படி, \(AC^2 = AB^2 + BC^2\).
எனவே, \(AB^2 = AC^2 - BC^2\).
\(\Rightarrow AB^2 = 29^2 -21^2\)
\(= 841 - 441\)
\(= 400\)
\(AB = \sqrt{400}\).
\(AB = 20\)
எனவே, மற்றொரு பக்கத்தின் நீளம் \(20\) செ.மீ.
