PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoசேர்ப்புக் கணத்தின் ஆதி எண்
A மற்றும் B இரு கணம் எனில், இதன் சேர்ப்புக் கணம் A \cup B. இந்த சேர்ப்புகணத்தின் ஆதி எண்ணை கண்டுபிடிக்க முடியுமா?
முடியும். A மற்றும் B இரு கணங்களில் உள்ள அனைத்து உறுப்புகளும் A \cup B இல் உள்ளன. எனவே, ஆகிய இரு கணங்களின் எண்ணிக்கையைக் கூட்ட வேண்டும்.
n(A \cup B) = n(A) + n(B)
இந்தக் கூற்று சரியா என்றால் இல்லை. எல்லா இடத்திலும் இது சரியாக இருக்காது. ஏனெனில், A மற்றும் B இரு கணங்களுக்கும் பொதுவான உறுப்புகள் சில இருக்கும். இவற்றைக் கூட்டும்போது அவ்வுறுப்புகள் இரு முறை இடம்பெறும். எனவே, இரு கணத்திற்கும் பொதுவான உறுப்புகளைக் (n(A \cap) கழிக்க வேண்டும்.
n(A \cup B) = n(A) + n(B) - n(A \cap B)
இதுவே, சேர்ப்புக் கணத்தின் ஆதி எண்ணைக் கண்டுபிடிக்க சரியான கூற்று ஆகும்.
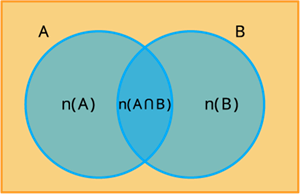
A மற்றும் B என்பன இரு முடிவுறு கணங்கள் எனில்:
(i) n(A \cup B) = n(A) + n(B) - n(A \cap B)
(ii) n(A \cap B) = n(A) + n(B) - n(A \cup B)
(iii) n(A - B) = n(A) - n(A \cap B)
(iv) n(B - A) = n(B) - n(A \cap B)
(v) n(A') = n(U) - n(A)
(vi) n(U) = n(A) + n(A')
(vii) A மற்றும் B என்பன வெட்டாக் கணங்கள் எனில், n(A \cup B) = n(A) + n(B).
Example:
A = \{1, 2, 3, 5\} மற்றும் B = \{2, 4, 5, 6, 7\} எனில், A \cup B இல் உள்ள உறுப்புகளின் எண்ணிக்கையைக் காண்க.
A = \{1, 2, 3, 5\}
n(A) = 4
B = \{2, 4, 5, 6, 7\}
n(B) = 5
A \cap B = \{2, 5\}
n(A \cap B) = 2
n(A \cup B) = n(A) + n(B) - n(A \cap B)
n(A \cup B) = 4 + 5 - 2
n(A \cup B) = 7
சரிபார்த்தல்:
A \cup B = \{1, 2, 3, 4, 5, 6, 7\}
n(A \cup B) = 7
Register for free to see more content