
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoSrinivasa Ramanujan was born in the late \(1880s \). During those times, the education system differed from the current system. He was initially enrolled in a primary school in Kumbakonam. But when he was sent to stay with his grandparents in Madras, he hated attending the school there. It went to the extent where a constable was appointed to ensure that he attended school daily, without missing it. In spite of this, Ramanujan insisted and was taken back to Kumbakonam, where he was enrolled in Towns Higher Secondary School, where he encountered formal Mathematics for the first time. He started taking an interest in the various mathematical problems posed by his teacher.
The lesson begins by pointing to a particular incident that took place within the classroom. Teachers generally make the class interactive to make it more interesting and easily understandable to the children. In Ramanujan's arithmetic class, the teacher handles the topic division. The division is a method of distributing things equally between someone. For example, if there are two people, and there are only two bananas, then if each person receives one each, it is an equal division.

Three bananas drawn on the blackboard
In the olden days, students did not have access to online learning or technological advancements such as ppt and audio-visual aids. The teachers most often drew or wrote on the blackboard, which was viewed by the entire class. It is easier to remember things when one sees them, especially in the form of pictures or videos. The concept taught along with it gets etched in the memory of little children. So The Maths teacher draws three bananas on the board and asks them the question of how they are supposed to distribute/ divide the three bananas amongst three people.

Division
When the teacher asks the class how one can divide three bananas amongst three people equally, a smart boy in the class immediately answers that if three bananas are equally divided amongst three people, then each one should get one banana. This proves to be the right answer, as any person in the group receiving two bananas or the whole bunch of three bananas would leave the rest with no bananas or lesser bananas. That would not be an equal distribution.
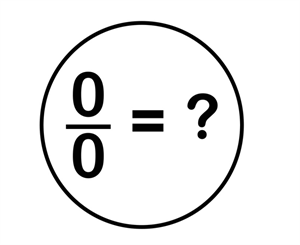
The boy's question
The teacher uses a small number to make the students understand the concept of division. She then goes on to use a bigger number like \(1000\) to prove that no matter how bigger the number gets, the concept remains the same. Even if one divides 1000 bananas amongst 1000 people, each person receives one each to make it an equal distribution.
As soon as the concept is explained, a boy raises his hand, indicating that he has a doubt. The teacher who encourages doubts in students, pauses to clarify the student's doubt. Doubts are signs that the concept has reached the student. The student asks if no banana is distributed, then will everyone receive one banana each. For example, if there are 3 bananas and three people, and no banana is distributed, will all the three people receive one banana each. The students laugh at the question as the question contradicts itself, as it states clearly that no banana is distributed. So the students wonder how a person can get one banana each when there is no bananas is distributed in reality. They laugh at the boy, thinking it is a silly question.

The Students are surprised and laughed at the boy
The students laugh at the boy as they think it is a very silly question to ask if no banana is distributed, then will everyone get one banana each. Although the boy's doubt was genuine and he did not ask it to stir up the class, his classmates do not understand the logic behind his doubt. But the teacher being an expert in the subject and well qualified, understands what he meant and explains it to the students.
The student had in fact understood what would happen when there is a specific number of items given and is asked to divide amongst a specific number of people. But he just wants to know how one is supposed to divide when there is no particular number of bananas to divide. The teacher explains the concept of dividing the same number by itself. Any number divided by itself is one. For example, three divided by three would be \(1\), Thousand divided by thousand is 1. Similarly, zero divided by zero would give infinite options. It also works under the concept of probability. If one divides zero bananas, then each person stands a chance of receiving as many number of bananas as possible.

The symbol for Infinity
When the teacher explains this to the students, they understand the tricks that arithmetic has played on them. One might easily be tricked into thinking that when no banana is distributed, no one will receive the banana, but the true fact is that it works on the chances of one receiving many bananas. But the boys being very young, did not understand the depth behind such a brilliant question. The question that was asked by the young boy was a huge concept that took a lot of Mathematicians to solve. The great Indian Mathematician Bhaskara was the one who solved and established that zero divided by zero is Infinity. The boy who had asked such a brilliant question was Srinivasa Ramanujan. All through his educational journey from his primary school in Kumbakonam to his days at Cambridge University, he was always ahead of his teachers.
Ramanujan, who was the brilliant boy who came with the question which later took great mathematicians a long while to solve, was enthusiastic about Maths from a very young age. He was born in Erode in Tamil Nadu on December \(22\), \(1887\). He was born before the Indian Independence and therefore was exposed to a different kind of education system. He went to an all boys school in Kumbakonam. He did not belong to a rich family and came from a moderate background. His father worked in a cloth shop. But his humble background did not stop him from researching or following his passion for Maths.
He was a genius and had a curious mind from a very early age. When his classmates were solving simple arithmetic like addition and subtraction, Ramanujan was solving the sums from the college syllabus. In fact students who were considerably elder to him and in higher classes solved their doubts with him. He lived in a dingy house, but it did not matter as Ramanujan's brilliance overshadowed all his poverty. He was a living proof that familial circumstances did not matter to sharpen one's knowledge.

A Dingy House in Kumbakkonam
At a very young age of \(13\), he visited college libraries as he wanted to expand his knowledge in Mathematics. He chanced upon a book called "Plane Trigonometry" by a famous Mathematician called S. L. Loney, which was published in 1912. Loney was a very early influence on Ramanujan as his books explained trigonometric equations easily. Trigonometry is a branch of Mathematics, which focuses on the relationship between the angles and side lengths of a triangle. Trigonometry is mostly used in making inclined roofs, to make maps, to analyze the height of buildings etc. Not only did Ramanujan explore Loney's book, but he also researched and introduced new theorems and formulae and added to it.
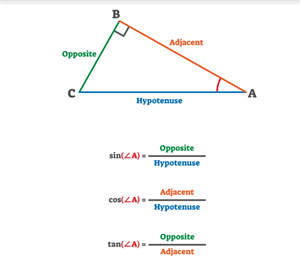
Trigonometry
At the age of \(13\), Ramanujan had cracked the difficult problems of trigonometry. No child of his age could even dream of doing the same. But his passion for Mathematics drove him to explore new areas in the subject. After two years, one of his senior friends introduced him to one of the best books for basic Mathematics, Synopsis of Elementary Results in Pure Applied Mathematics, by a famous British Mathematics George Shoobridge Carr. He includes all kinds of basic solutions to all kinds of problems to help students prepare for degree-level examinations such as the Cambridge Mathematical students.
Ramanujan had in fact started his pursuit for Cambridge at such a tender age. In fact, the book proved as a base level introduction for him, which helped him reach Cambridge in the future. The title itself is a lengthy one that includes conceptual terms. Rather than getting scared by it, he found it as a blessing and it proved as a trigger for the mathematical genius in him. He started working on all the problems and gained bliss out of it. When students of his age gained entertainment out of cartoons and games, Ramanujan considered Maths as his entertainment. He solved the problems like a game.

Ramanujan loved solving Maths
The book gave him new ideas and it started overflowing with solutions and theorems. Since it was brimming in his mind, he was not able to write it all down at once. He jotted down in pieces of paper or loose sheets of paper that lay around him. Since one cannot always carry a notebook with them, he wrote on slates or anything that was available to him, as he was not ready to forget or let go of the thought. Before he went abroad for his higher studies, he had filled three notebooks of his ideas, which later came to be known as Ramanujan’s Frayed Notebooks. He had rightly named it so, as frayed generally refers to anything that is disarranged, loose or hanging about.

Loose Papers
Ramanujan was interested in Mathematics and scored really well in school. He had no problem in cracking any exams as he was way ahead of his classmates and all other students of his age. He had read all books on the subject and had even made new ideas and theorems. But no human being in this world can claim to know everything and to be perfect. If one person is good at Maths, the other may be good at arts. Similarly, if one is good at dance, the other may be good at writing poetry. Each one should identify their talents, work on it and become the best in the selected area. But unfortunately for Ramanujan, the Indian education system passed off their students only if they perform equally in all the subjects.

He failed in other subjects
Since Ramanujan spent most of his time in Maths, he did not concentrate on other subjects like Arts, Science, Physiology, English and history. He failed in the examinations. He had even gained the Subramanyam award for Maths. But when he enrolled himself in the Pachaiyappas College, Madras, he failed twice because he could not perform well in other subjects. Just like any other parent, Ramanujan's father was also disappointed with this. From his perspective, he could only see that his boy was always scribbling on random papers. He could not understand the passion Ramanujan possessed, rather thought he had gone mad, as he was obsessed with Maths.

Ramanujan always solved maths
As he struggled to get a degree, he had to search for a job to sustain his life in Madras. He wanted to earn, most importantly for papers to write upon. If he did not write in papers, he might lose his ideas. It was more important to him than food. In order to do his calculations, he needed almost \(2000\) sheets of paper. That is how much he worked on various problems. In order to save paper, he started using scraps of old papers that he found unused, lying on the streets.
Most people need more papers because they need to correct their mistakes. It is not necessary that one should always get the right solution in the first attempt. But Ramanujan could not afford to use a different set of paper for his corrections. So he used a different colour pen and overwrote what he had already written in blue. That way, he did not have to use more papers. He also used the papers which were already written in blue by writing over them in red ink.
Ramanujan found it difficult to lead a very normal life like others as he was not recognized for his work. His passion for Maths was not well received, as he had no particular degree. He had to survive, feed himself, and take care of himself. He was left alone to fend for himself. He did not concentrate more on dressing and hygiene. What little time he had, he spent on solving Maths. He, therefore, looked unkempt and uncouth.

An Unkempt man
In an attempt to get a clerical job, he kept showing his frayed notebooks to everyone that he knew. But no one could match the level of Ramanujan's intellect in Maths. It is an example of how certain things do not happen in life, not because one is not capable, but just because one is simply not understood. All his applications are turned down as one understands his complicated theories. It proves to be too difficult for them, but they turn it down because they do not understand its value.
After a long struggle, Ramanujan was finally recognized by the Director of Madras Port Trust, Francis Spring. The Madras port was a place ships were docked. It showed that no man experiences sorrow throughout his life or happiness all through life. Thus Ramanujan's sorrows came to an end and a ray of hope shines in his life. His first salary working as a clerk in the port was \(₹25\). It was a good amount before the Independence. However, he moved further in his life when he worked really well with the finances and calculations and gained recognition from teachers and educationalists. Finally, his hard work paid off when the University of Madras granted him a fellowship of \(₹75\) a month, though he had no qualifying degree. A fellowship is when the student could conduct his research and still get paid. He was awarded the fellowship on May \(1\), \(1913\), after many years of not getting recognition and being ignored.

Port
Ramanujan was a very determined person. He did not give up on his dreams and settle for less when he failed in his exams. At the same time, he was practical enough to get a clerical job to sustain himself and work on his skills. Whilst he was working and completing his research at Madras University, he felt the need to reach greater heights. He aimed for the highest as he sent a letter to the great Mathematician G.H. Hardy of Cambridge University.
He is a perfect example of how one must not belittle themselves after a failure. Any person in his position would have easily given up after two consecutive failures. But Ramanujan understood that he was good at Maths and that it could take him to greater levels. He did not bother about the ones that he was not good at, and instead, he focussed on sharpening his skills in Maths and exploring all areas possible. Cambridge was the best institution of the time, and he sent all his \(120\) theorems and formulae that he had worked on throughout his years. Among the formulae was a very famous series called the Reimann series, which was very important in a topic called Integral Calculus. Integral calculus deals with total size or value, such as lengths, areas, and volumes. But since it was an age without social media or the internet, he was not aware of the fact that his formulae was already solved by a German Mathematician named George F. Reimann. The series was even named after him. But Ramanujan had cracked such a rare series at a very young age, which Reimann had taken years to complete. Ramanujan had worked on the series without being aware of it existing already, which showed that he was capable of great things.

Calculus
He also included a type of equations called "Modular". Although this equation was only a hypothesis, Pierre Deligne, another great Mathematician, proved it to be right. As soon as the letters reached Hardy and his colleague J.E. Littlewood, they understood that they had found a genius. The equations that took their own men who were trained them, was solved by a person who had no proper training or degree. Ramanujan researched and most of his theories were based on self-learning. They immediately contacted Ramanujan and made arrangements to move from India and reach Cambridge in Britain. He set sail for Britain on March \(17\), \(1914\), which proved as a life-changing experience for him.
Hardy selected Ramanujan to do his research in Cambridge. Ramanujan, having born into a poor family in Erode, was not exposed to a different lifestyle. India, which was under British control during his times, was still striving to maintain its culture, regardless of the foreign influence. In India, he was brought up in a strictly conservative family, where he had to follow norms and keep up the rules. He was a strict vegetarian and found it difficult to cope with the eating habits of Britain. The climate was completely different in Britain, and people had to eat meat to sustain the cold. He could not bear the cold of the country as India was a tropical country and Madras experienced more of Summer. But none of this stopped Ramanujan from focussing on Maths. He started cooking his own food. He also had Hardy and Littlewood for the company. They helped him curb his loneliness.

He cooked for himself
Hardy noticed in Ramanujan, a very unsystematic mathematician. For example, he knew what the Pythagoras theorem was but did not know about the congruent triangle. The Pythagoras triangle simply states that, in a right-angled triangle, the square of the longest side (also called the hypotenuse of the triangle) is equal in area to the sum of the squares of the other two sides of the triangle. If the hypotenuse is \(C\), then the Pythagoras theorem states that \(a2 + b2 = c2\). A congruent triangle is one in which all sides and angles are exactly the same. It is highly unlikely for a person who knows a hard concept like Pythagoras to not know about the congruent triangle, as they both deal with triangles. But Ramanujan lacked formal education.
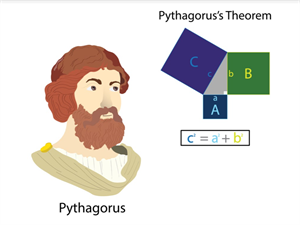
Pythagoras theorem
He did not consider Maths as a serious concept, and instead, he was in love with Maths. He experimented with it. He enjoyed solving problems and deriving equations. His brain worked in a marvellous way that he just solved and derived everything but did not prove it. He did not work on rigid matters like that. He left it for the people who were only worried about proofs, evidence and theories. Ramanujan was interested only in the mathematical truths and connected them to the universal laws.
Ramanujan was the best research candidate in Cambridge, that he was awarded a fellowship of the Royal Society. This fellowship is usually awarded only for scientists, physicists and mathematicians who have done the best research work. The university pays them to complete their research as it is a huge contribution to the society. In October, he became the first Indian to be elected Fellow of Trinity College, Cambridge. It was very rare that non-natives get a fellowship. But Ramanujan's work was highly appreciated by everyone. He worked with other scientists and colleagues like Hardy and Littlewood. They formed learning groups and worked on number theories and composite numbers. He and Roger worked on a list of the highest composite numbers. Composite numbers are numbers that are divisible by other numbers. For example, the number \(8\) is divisible by \(2\) and \(4\), as \(2×4\) is \(8\), and vice versa. He even contributed in the field of Algebra, equally in comparison to the godfathers of algebra Leonard Euler and Jacobi.
Ramanujan was diagnosed with tuberculosis. Back in the day, it was a very incurable disease like cancer. It could also be because of the cold climate in Britain. It affects the lungs of a person. He was sent back to India. But the disease had spread so much that he looked pale and tired when he reached. But rather than leaving behind everything, he still resorted to Maths as a medicine. He used to work on Maths, to ignore the pain and forget everything. He even played with numbers in his death bed. That was how much he loved Maths.

He worked on Maths in spite of being sick
Since Maths is related to astrology in a way, he used to give lectures regarding that. He gave lectures on topics such as “God, Zero and Infinity". He connected how God and infinity is the same, an unknown presence in everyone's lives.