UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreIn the earlier classes, we have learnt what circles and the terms related to the circle are. Now, let us analyse what happens if a circle and a line are on a plane.
Let us discuss some situations when a circle and a line intersect.
Situation 1: The line \(AB\) does not touch the circle.
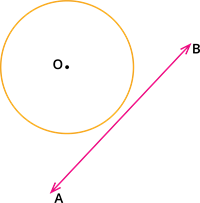 |
Here, there is no common point between the straight line \(AB\) and the circle.
Therefore, the number of points of intersection is zero.
Situation 2: The line \(AB\) touches the circle at one point.
 |
Here, there is one common point \(P\) between the straight line \(AB\) and the circle.
The line \(AB\) is called the tangent to the circle at \(P\).
Therefore, the number of points of intersection is one.
Situation 3: The line \(AB\) touches the circle at two points.
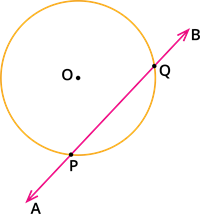 |
Here, there are two common points \(P\) and \(Q\) between the straight line \(AB\) and the circle.
The line \(AB\) is called the secant of the circle.
Therefore, the number of points of intersection is two.
Important!
The line segment inscribed in a circle is called the chord of the circle.
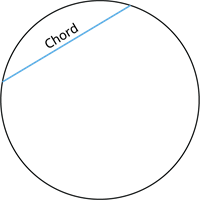 |
The chord is a sub-section of a secant.