
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoA trigonometric identity is an equation containing trigonometric ratios of an angle that is true for all values of the angle(s) involved.
Fundamental identities of trigonometry:
(1) \(\sin^2 \theta + \cos^2 \theta = 1\)
(2) \(1 + \tan^2 \theta = \sec^2 \theta\)
(3) \(1 + \cot^2 \theta = \text{cosec}^2\: \theta\)
We will prove these basic trigonometric identities.
\(\sin^2 \theta + \cos^2 \theta = 1\)
Consider a right triangle \(ABC\) with angle \(\theta\).
\(\sin \theta = \frac{AB}{AC}\) - - - - - (I)
\(\cos \theta = \frac{BC}{AC}\) - - - - - (II)
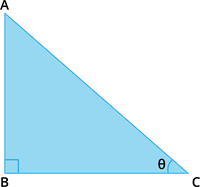
By Pythagoras theorem:
\(AB^2 + BC^2 = AC^2\)
Divide by \(AC^2\) on both sides.
\(\frac{AB^2}{AC^2} + \frac{BC^2}{AC^2} = \frac{AC^2}{AC^2}\)
\(\left(\frac{AB}{AC}\right)^2 + \left(\frac{BC}{AC}\right)^2 = \left(\frac{AC}{AC}\right)^2\)
\((\sin \theta)^2 + (\cos \theta)^2 = 1^2\) [using equation (I) and (II)]
\(\sin^2 \theta + \cos^2 \theta = 1\)
Hence, the identity is \(\sin^2 \theta + \cos^2 \theta = 1\).
\(1 + \tan^2 \theta = \sec^2 \theta\)
Consider a right triangle \(ABC\) with angle \(\theta\).
\(\tan \theta = \frac{AB}{BC}\) - - - - - (III)
\(\sec \theta = \frac{AC}{BC}\) - - - - - (IV)

By Pythagoras theorem:
\(AB^2 + BC^2 = AC^2\)
Divide by \(BC^2\) on both sides.
\(\frac{AB^2}{BC^2} + \frac{BC^2}{BC^2} = \frac{AC^2}{BC^2}\)
\(\left(\frac{AB}{BC}\right)^2 + \left(\frac{BC}{BC}\right)^2 = \left(\frac{AC}{BC}\right)^2\)
\((\tan \theta)^2 + 1^2 = (\sec \theta)^2\) [using equation (III) and (IV)]
\(\tan^2 \theta + 1 = \sec^2 \theta\)
Hence, the identity is \(1 + \tan^2 \theta = \sec^2 \theta\).
\(1 + \cot^2 \theta = \text{cosec}^2\: \theta\)
Consider a right triangle \(ABC\) with angle \(\theta\).
\(\cot \theta = \frac{BC}{AB}\) - - - - - (III)
\(\text{cosec}\: \theta = \frac{AC}{AB}\) - - - - - (IV)

By Pythagoras theorem:
\(AB^2 + BC^2 = AC^2\)
Divide by \(AB^2\) on both sides.
\(\frac{AB^2}{AB^2} + \frac{BC^2}{AB^2} = \frac{AC^2}{AB^2}\)
\(\left(\frac{AB}{AB}\right)^2 + \left(\frac{BC}{AB}\right)^2 = \left(\frac{AC}{AB}\right)^2\)
\(1^2 + (\cot \theta)^2 = (\text{cosec}\: \theta)^2\) [using equation (III) and (IV)]
\(1 + \cot^2 \theta + 1 = \text{cosec}^2\: \theta\)
Hence, the identity is \(1 + \cot^2 \theta + 1 = \text{cosec}^2\: \theta\).
Equal forms of trigonometric identities
Identity | Equal form of identity |
| \(\sin^2 \theta + \cos^2 \theta = 1\) | \(\sin^2 \theta = 1 - \cos^2 \theta \) (or) \(\cos^2 \theta = 1 - \sin^2 \theta\) |
| \(1 + \tan^2 \theta = \sec^2 \theta\) | \(\tan^2 \theta = \sec^2 \theta - 1\) (or) \(\sec^2 \theta - \tan^2 \theta = 1\) |
| \(1 + \cot^2 \theta = \text{cosec}^2\: \theta\) | \(\cot^2 \theta = \text{cosec}^2\: \theta - 1\) (or) \(\text{cosec}^2\: \theta - \cot^2 \theta = 1\) |
Important!
The three trigonometric identities are true for every \(\theta\) lies between \(0^\circ\) and \(90^\circ\).