PDF chapter test TRY NOW
We will derive the trigonometric ratios of \(90^{\circ}\) using the right angled triangle \(ABC\).
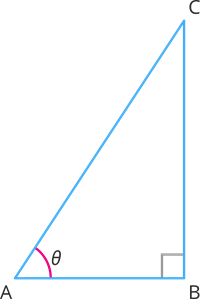
Let us now experiment with the given triangle concerning \(\angle A\).
Increase the value of \(\theta\) to the extent it becomes \(90\) degree.
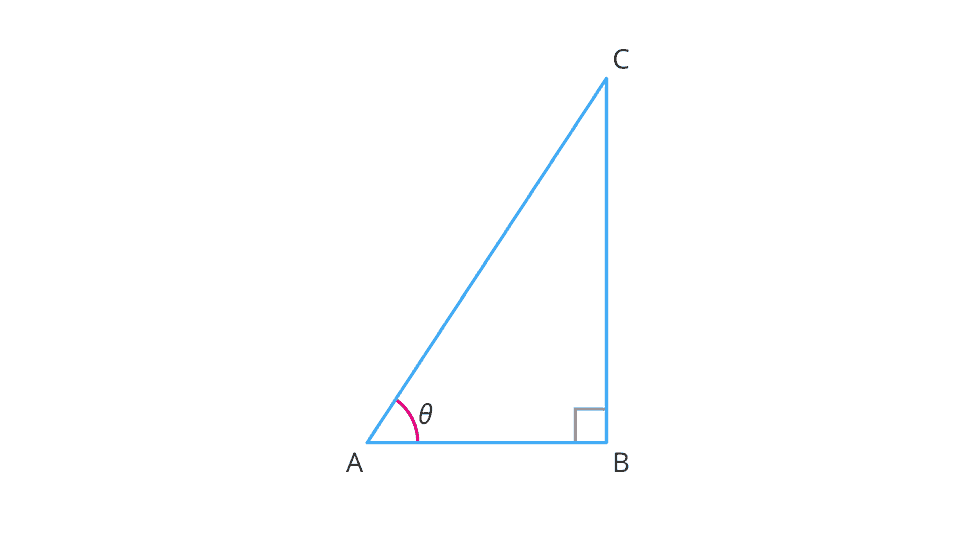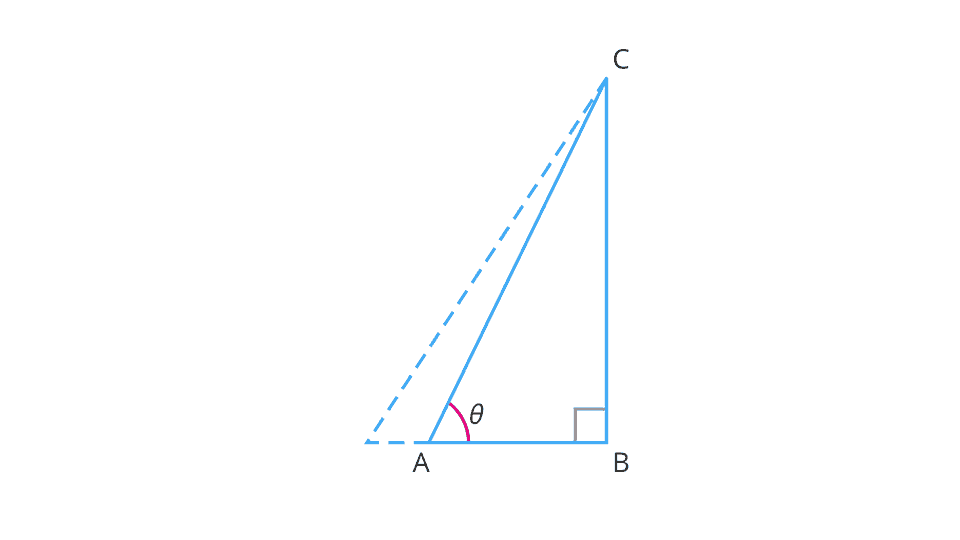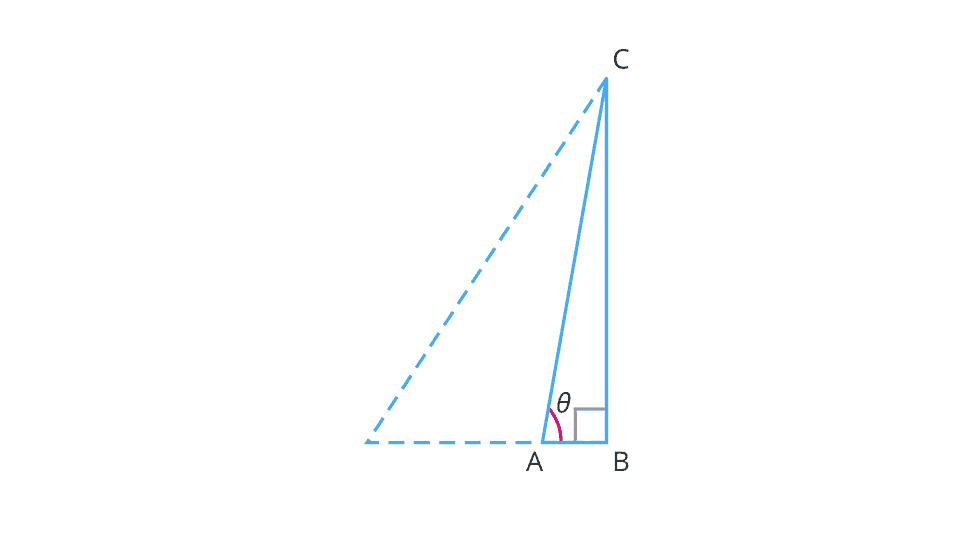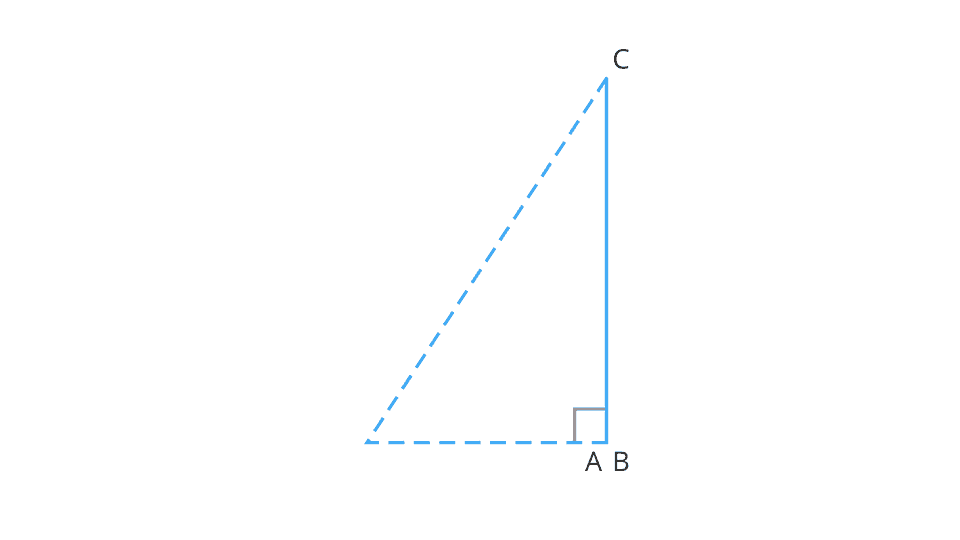
It is observed that as \(\angle A\) gets larger and larger, the point \(A\) gets closer to the point \(B\).
That is, when \(\theta\) becomes very close to \(90^{\circ}\), the side \(AC\) becomes at most the same as the side \(BC\).
This implies that the measure of \(AB\) becomes almost zero.
In the right angles triangle \(ABC\) we have:
Opposite side \(=\) \(BC\)
Adjacent side \(=\) \(AB\)
Hypotenuse \(=\) \(AC\)
Now, let us determine the trigonometric ratios when \(\theta = 90^{\circ}\) as follows.
- Sine \(90^{\circ}\):
\(\sin \theta\) \(=\) \(\frac{\text{Opposite side}}{\text{Hypotenuse}}\)
\(\sin \theta\) \(=\) \(\frac{BC}{AC}\)
\(\sin 90^{\circ}\) \(=\) \(1\) [When \(\angle A = 90^{\circ}\), \(AC\) \(=\) \(BC\).]
- Cosine \(90^{\circ}\):
\(\cos \theta\) \(=\) \(\frac{\text{Adjacent side}}{\text{Hypotenuse}}\)
\(\cos \theta\) \(=\) \(\frac{AB}{AC}\)
\(\cos 90^{\circ}\)\(=\) \(\frac{0}{AC}\)
\(=\) \(0\)
- Tangent \(90^{\circ}\):
\(\tan 90^{\circ}\) \(=\) \(\frac{\sin 90^{\circ}}{\cos 90^{\circ}}\)
\(=\) \(\frac{1}{0}\)
\(=\) not defined
Using these basic trigonometric ratios determine their reciprocals as follows:
- Cosecant \(90^{\circ}\):
\(\text{cosec}\,90^{\circ}\) \(=\) \(\frac{1}{\sin 90^{\circ}}\)
\(=\) \(\frac{1}{1}\)
\(=\) \(1\)
- Secant \(90^{\circ}\):
\(\sec 90^{\circ}\) \(=\) \(\frac{1}{\cos 90^{\circ}}\)
\(=\) \(\frac{1}{0}\)
\(=\) not defined
- Cotangent \(90^{\circ}\):
\(\cot 90^{\circ}\) \(=\) \(\frac{1}{\tan 90^{\circ}}\)
\(=\) \(\frac{0}{1}\)
\(=\) \(0\)
Let us summarize all the trigonometric ratios of \(90^{\circ}\) in the following table.
\(\sin \theta\) | \(\cos \theta\) | \(\tan \theta\) | \(\text{cosec}\,\theta\) | \(\sec \theta\) | \(\cot \theta\) | |
\(\theta = 90^{\circ}\) | \(1\) | \(0\) | not defined | \(1\) | not defined | \(0\) |
Register for free to see more content