UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreConsider an equilateral triangle \(ABC\) with sides measuring \(2\) units.
That is \(AB\) \(=\) \(BC\) \(=\) \(CA\) \(=\) \(2\) units.
Draw a bisector of \(\angle A\) such that it meets \(BC\) at \(D\).
The angle bisector of an equilateral triangle also bisects the side opposite it.
So, \(BD\) \(=\) \(DC\) \(=\) \(1\) unit.
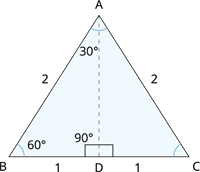
First, let us calculate the measure of angle bisector \(BD\) in the figure.
Consider the triangle \(ABD\).
Since the given triangle is a right-angled triangle by the Pythagoras theorem, we have:
In a right angled triangle, \(\text{Hypotenuse}^{2} = \text{Adjacent side}^{2} + \text{Opposite side}^{2}\).
\(AB^2\) \(=\) \(BD^2\) \(+\) \(DA^2\).
\(DA^2\) \(=\) \(AB^2\) \(-\) \(BD^2\)
\(DA^2\) \(=\) \(2^2\) \(-\) \(1^2\)
\(DA^2\) \(=\) \(4 - 1\)
\(DA^2\) \(=\) \(3\)
\(\Rightarrow DA\) \(=\) \(\sqrt{3}\)
Therefore, for the considered right-angled triangle, we have:
| With respect to \(30^{\circ}\) | With respect to \(60^{\circ}\) |
| Opposite side \(=\) \(1\) units | Opposite side \(=\) \(\sqrt{3}\) units |
| Adjacent side \(=\) \(\sqrt{3}\) units | Adjacent side \(=\) \(1\) units |
| Hypotenuse \(=\) \(2\) units | Hypotenuse \(=\) \(2\) units |
Now, let us determine all the trigonometric ratios of \(30^{\circ}\) and \(60^{\circ}\).
- Sine:
\(\sin 30^{\circ}\) | \(\sin 60^{\circ}\) |
\(\sin 30^{\circ}\) \(=\) \(\frac{\text{Opposite side}}{\text{Hypotenuse}}\) \(=\) \(\frac{1}{2}\) | \(\sin 60^{\circ}\) \(=\) \(\frac{\text{Opposite side}}{\text{Hypotenuse}}\) \(=\) \(\frac{\sqrt{3}}{2}\) |
- Cosine \(30^{\circ}\):
\(\cos 30^{\circ}\) | \(\cos 60^{\circ}\) |
\(\cos 30^{\circ}\) \(=\) \(\frac{\text{Adjacent side}}{\text{Hypotenuse}}\) \(=\) \(\frac{\sqrt{3}}{2}\) | \(\cos 60^{\circ}\) \(=\) \(\frac{\text{Adjacent side}}{\text{Hypotenuse}}\) \(=\) \(\frac{1}{2}\) |
- Tangent:
\(\tan 30^{\circ}\) | \(\tan 60^{\circ}\) |
\(\tan 30^{\circ}\) \(=\) \(\frac{\text{Opposite side}}{\text{Adjacent side}}\) \(=\) \(\frac{1}{\sqrt{3}}\) | \(\tan 60^{\circ}\) \(=\) \(\frac{\text{Opposite side}}{\text{Adjacent side}}\) \(=\) \(\frac{\sqrt{3}}{1}\) \(=\) \(\sqrt{3}\) |
Using these basic trigonometric ratios determine their reciprocals as follows:
- Cosecant:
\(\text{cosec}\,30^{\circ}\) | \(\text{cosec}\,60^{\circ}\) |
\(\text{cosec}\,30^{\circ}\) \(=\) \(\frac{1}{\sin 30^{\circ}}\) \(=\) \(\frac{2}{1}\) \(=\) \(2\) | \(\text{cosec}\,60^{\circ}\) \(=\) \(\frac{1}{\sin 60^{\circ}}\) \(=\) \(\frac{2}{\sqrt{3}}\) |
- Secant:
\(\sec 30^{\circ}\) | \(\sec 60^{\circ}\) |
\(\sec 30^{\circ}\) \(=\) \(\frac{1}{\cos 30^{\circ}}\) \(=\) \(\frac{2}{\sqrt{3}}\) | \(\sec 60^{\circ}\) \(=\) \(\frac{1}{\cos 60^{\circ}}\) \(=\) \(\frac{2}{1}\) \(=\) \(2\) |
- Cotangent:
\(\cot 30^{\circ}\) | \(\cot 60^{\circ}\) |
\(\cot 30^{\circ}\) \(=\) \(\frac{\text{1}}{\tan 30^{\circ}}\) \(=\) \(\frac{\sqrt{3}}{1}\) \(=\) \(\sqrt{3}\) | \(\cot 60^{\circ}\) \(=\) \(\frac{\text{1}}{\tan 60^{\circ}}\) \(=\) \(\frac{1}{\sqrt{3}}\) |
Let us summarize all the trigonometric ratios of \(30^{\circ}\) and \(60^{\circ}\) in the following table.
\(\sin \theta\) | \(\cos \theta\) | \(\tan \theta\) | \(\text{cosec}\,\theta\) | \(\sec \theta\) | \(\cot \theta\) | |
\(\theta = 30^{\circ}\) | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{3}}\) | \(2\) | \(\frac{2}{\sqrt{3}}\) | \(\sqrt{3}\) |
\(\theta = 60^{\circ}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{2}\) | \(\sqrt{3}\) | \(\frac{2}{\sqrt{3}}\) | \(2\) | \(\frac{1}{\sqrt{3}}\) |
Register for free to see more content