PDF chapter test TRY NOW
Trigonometry (originated from the Greek word tri means three, gon means sides and, metron means measure) is a branch of mathematics that deals with the study of relationships involving the length of sides and angles of triangles.
Trigonometric Ratios:
Consider a right-angled triangle with a corresponding angle \(\theta\).
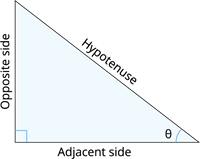
In the figure, the side opposite to the given angle \(\theta\) is called the 'Opposite side', the side adjacent to the given angle \(\theta\) is called the 'Adjacent side', and the greatest side opposite to right angle is called the 'hypotenuse'.
Important!
Click here! To recall the Pythagoras theorem. (Since we frequently make use of the right-angled triangle.)
Based on the corresponding angle \(\theta\), we will learn about three basic trigonometric ratios satisfied by a right-angled triangle.
Each of these ratios is obtained by dividing one side of the right-angled triangle by another.
The three basic trigonometric ratios are:
- Sine
- Cosine
- Tangent
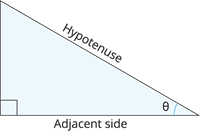
The table below depicts the relation of these ratios with the right-angled triangle.
| Name of the angle |
Sine
|
Cosine
|
Tangent
|
| Short form of the angle |
\(\sin\)
|
\(\cos\)
|
\(\tan\)
|
| Measurements related to the right-angled triangle |
 |
 |
 |
| Relationship |
\(\sin \theta\) \(=\) \(\frac{\text{Opposite side}}{\text{Hypotenuse}}\)
|
\(\cos \theta\) \(=\) \(\frac{\text{Adjacent side}}{\text{Hypotenuse}}\)
|
\(\tan \theta\) \(=\) \(\frac{\text{Opposite side}}{\text{Adjacent side}}\)
|
Important!
1. The trigonometric ratios are unitless as they are defined in terms of ratios of sides of the triangle.
2. The ratios \(\sin \theta\), \(\cos \theta\) and \(\tan \theta\) should not be treated as \((\sin) \times (\theta)\), \((\cos) \times (\theta)\) and \((\tan) \times (\theta)\).
3. \(\left(\sin \theta\right)^2\) should not be treated as \(\sin \theta^2\) or \(\sin^2 \theta^2\).
4. Trigonometric ratios depend only on the value of \(\theta\) and are independent of the lengths of the sides of the right angled triangle.
Register for free to see more content