Graphical Method of Solution of a Pair of Linear Equations

UPSKILL MATH PLUS

Learn Mathematics through our AI based learning portal with the support of our Academic Experts!

Let us learn how to find the solution of a pair of linear equations graphically.

Example:

1. Jane bought $2$ apples and $1$ banana for the cost of $$8$. Also, the cost of a banana is twice the cost of an apple. Represent this situation algebraically and graphically.

Solution:

Let $x$ denotes the cost of an apple and $y$ denote the cost of a banana.

The pair of equations are:

$2x + y = 8$ ---- ($1$)

$y = 2x$ ---- ($2$)

Graphical representation:

To represent the equations graphically, we need atleast $2$ solutions of these equations.

Consider the below table for the equation $2x + y = 8$.

$x$	$0$	$2$	$4$
$y = 8 - 2x$	$8$	$4$	$0$

Similarly, consider the below table for the equation $y = 2x$.

$x$	$0$	$2$	$4$
$y = 2x$	$0$	$4$	$8$

Now, plot the points $(0,8)$, $(2,4)$ and $(4,0)$ and draw a line joining these points and name it as the equation $2x + y = 8$.

Similarly, plot the points $(0,0)$, $(2,4)$ and $(4,8)$ and draw a line joining these points and name it as the equation $y = 2x$.

Therefore, the graph looks like this:

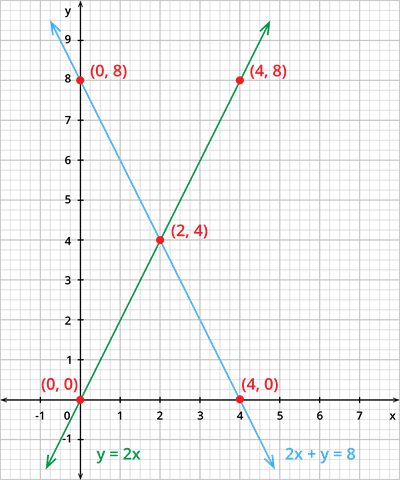
From the graph, we can see that the two lines intersect at the point $(2,4)$.

Algebraic representation:

Let us verify algebraically that $(2,4)$ is the solution of the given pair of linear equations.

Substituting $x = 2$ and $y = 4$ in equations ($1$) and ($2$), we get:

$\text{LHS} = 2x + y = 2(2) + 4 = 8 = \text{RHS}$

$\text{LHS} = y - 2x = 4 - 2(2) = 4 - 4 = 0 = \text{RHS}$

Therefore, $(2,4)$ is the solution of the given pair of equations.

Hence, the cost of an apple is $$2$, and the cost of a banana is $$4$.

2. Find the solution to the system of equations $2x + y = 8$ and $4x + 2y = 10$ graphically and algebraically.

Solution:

The two equations are:

$2x + y = 8$ ---- ($1$)

$4x + 2y = 10$ ---- ($2$)

Graphical representation:

Consider the below table for the equation $2x + y = 8$.

$x$	$1$	$2$	$3$	$4$
$y$	$6$	$4$	$2$	$0$

Similarly, consider the below table for the equation $4x + 2y = 10$.

$x$	$0$	$1$	$2$	$3$
$y$	$5$	$3$	$1$	$-1$

Now, plotting these points in the graph, we get:

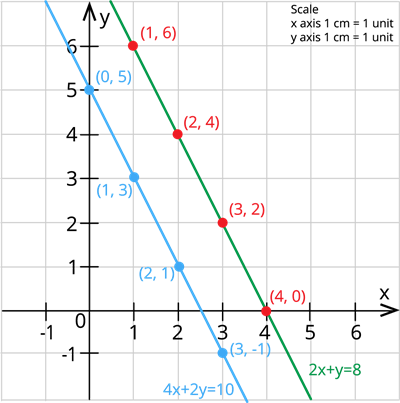
Since the two lines in the graph do not intersect, the two lines are parallel.

Algebraic representation:

From the graph, we can see that the two lines do not intersect. This means that the equations have no common point.

3. Find the solution to the system of equations $2x + y = 8$ and $4x + 2y = 16$.

Solution:

The two equations are:

$2x + y = 8$ ---- ($1$)

$4x + 2y = 16$ ---- ($2$)

Graphical representation:

Consider the below table for the equation $2x + y = 8$.

$x$	$0$	$2$	$4$
$y$	$8$	$4$	$0$

Similarly, consider the below table for the equation $4x + 2y = 16$.

$x$	$0$	$2$	$4$
$y$	$8$	$4$	$0$

Now, plotting these points in the graph, we get:

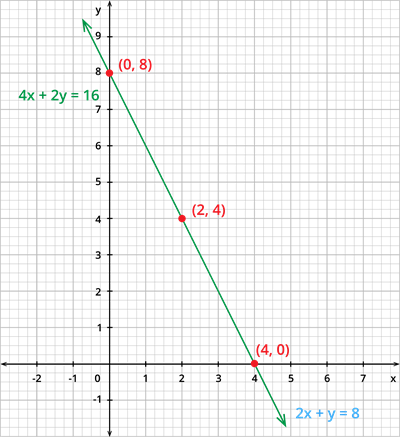
Algebraic representation:

This graph shows that both the equations have every point on the line is a common solution of these equations. This implies that these two equations have infinitely many solutions.

Previous theory

Exit to the topic

Next theory

Send feedback

Did you find an error?

Send it to us!

\(x\)	\(0\)	\(2\)	\(4\)
\(y = 8 - 2x\)	\(8\)	\(4\)	\(0\)

\(x\)	\(0\)	\(2\)	\(4\)
\(y = 2x\)	\(0\)	\(4\)	\(8\)

\(x\)	\(1\)	\(2\)	\(3\)	\(4\)
\(y\)	\(6\)	\(4\)	\(2\)	\(0\)

\(x\)	\(0\)	\(1\)	\(2\)	\(3\)
\(y\)	\(5\)	\(3\)	\(1\)	\(-1\)

\(x\)	\(0\)	\(2\)	\(4\)
\(y\)	\(8\)	\(4\)	\(0\)

3. Graphical Method of Solution of a Pair of Linear Equations

Theory: