UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreConsider a scenario of tossing a coin.
Either we get a head, or a tail is equally likely to appear. In other words, we can say the probabilities of both events are equal.
That is, P(getting a head) \(= \frac{1}{2}\)
P(getting a tail) \(= \frac{1}{2}\)
Similarly, let us consider another example of throwing a dice.
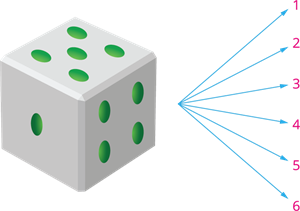
A dice has six faces, and their possible outcomes are \(1\), \(2\), \(3\), \(4\), \(5\) and \(6\). On throwing a dice, we may end up in any one of the six faces. That is, on throwing a dice, the equally likely events are \(1\), \(2\), \(3\), \(4\), \(5\) and \(6\).
In this chapter, we shall learn how to solve the problems when they are equally likely.
Important!
The empirical or experimental probability \(P(E)\) of an event \(E\) is defined as:
\(P(E) = \frac{\text{Number of trials in which the event happened}}{\text{Total number of trials}}\)
The theoretical probability or classical probability of an event \(E\) is defined as:
\(P(E) = \frac{\text{Number of outcomes favourable to E}}{\text{Number of all possible outcomes of the experiment}}\)
Note that \(0 \leq P(E) \leq 1\)
Register for free to see more content