
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoTheorem:
Every composite number can be expressed (factorised) as a product of primes, and this factorisation is unique, apart from the order in which the prime factors occur.
Explanation:
Let us take the composite number \(N\).
Decompose the number \(N\) into the product of primes.
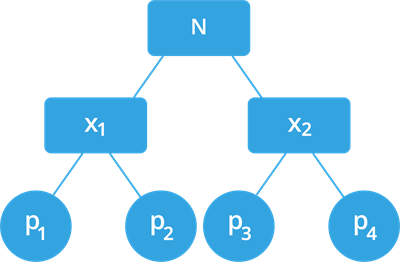
Here, the number \(N = x_1 \times x_2\). But, both \(x_1\) and \(x_2\) are again a composite number. So, factorise it further to obtain a prime number.
The prime factors of \(x_1 = p_1 \times p_2\).
The prime factors of \(x_2 = p_3 \times p_4\).
We get, \(N = p_1 \times p_2 \times p_3 \times p_4\) where \(p_1\), \(p_2\), \(p_3\) and \(p_4\) are all prime numbers.
If we have repeated primes in a product, then we can write it as powers.
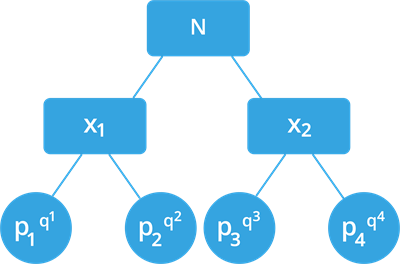
In general, given a composite number \(N\), we factorise it uniquely in the form where are prime numbers, and are natural numbers.
Thus, every composite number can be expressed as a product of primes apart from the order.
Example:
Consider a composite number \(26950\).
Let us factor this number using the factor tree method.
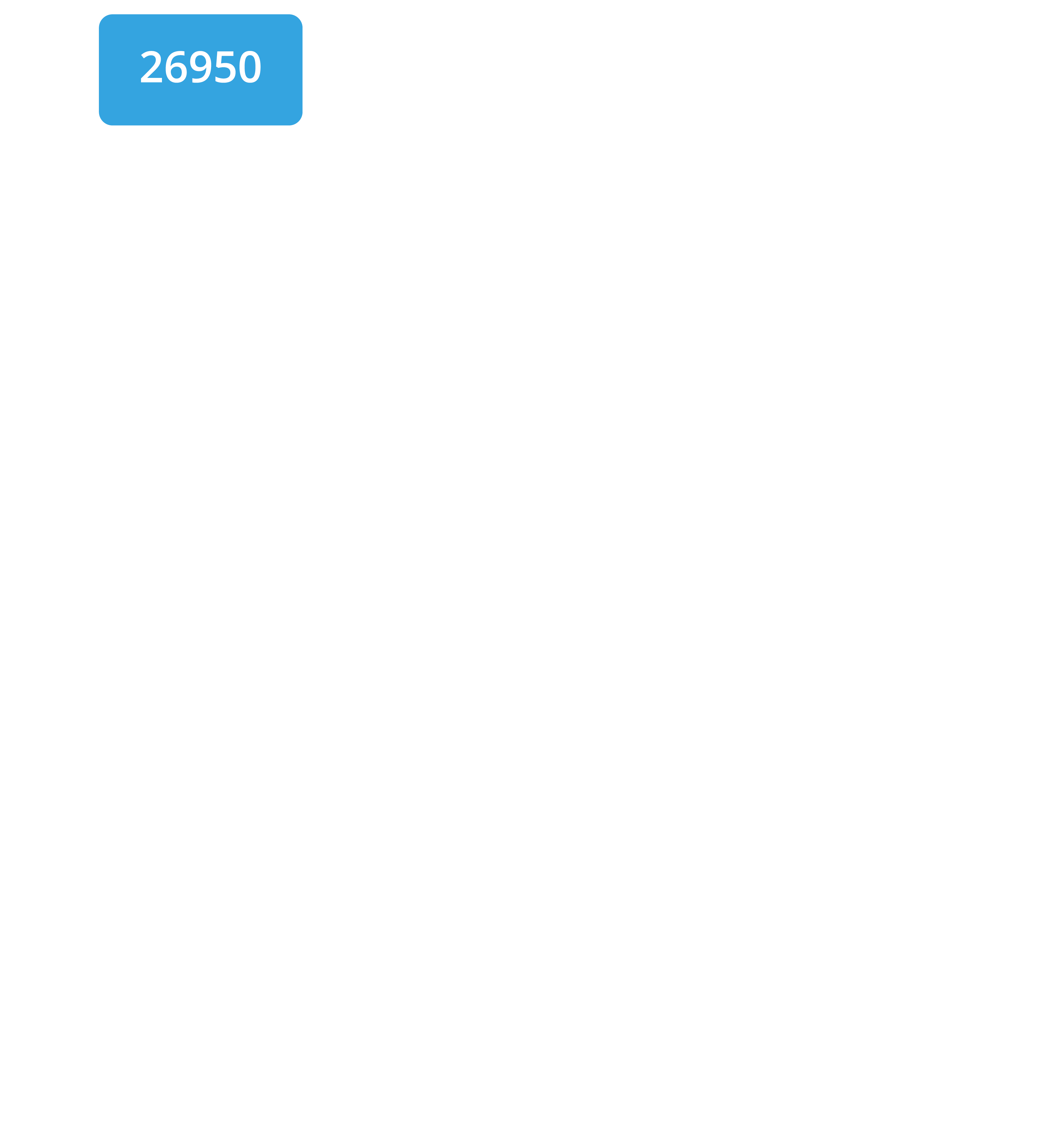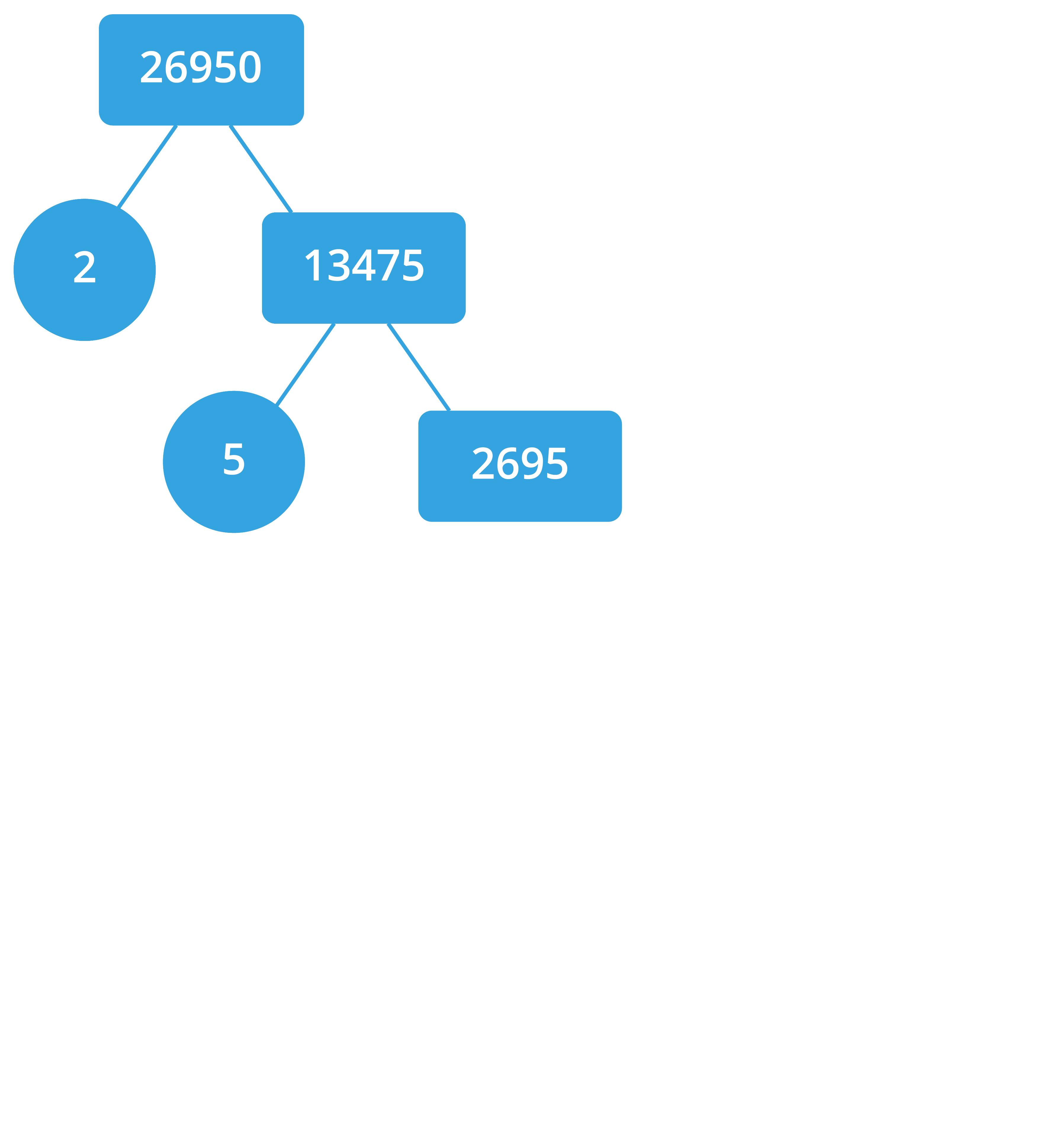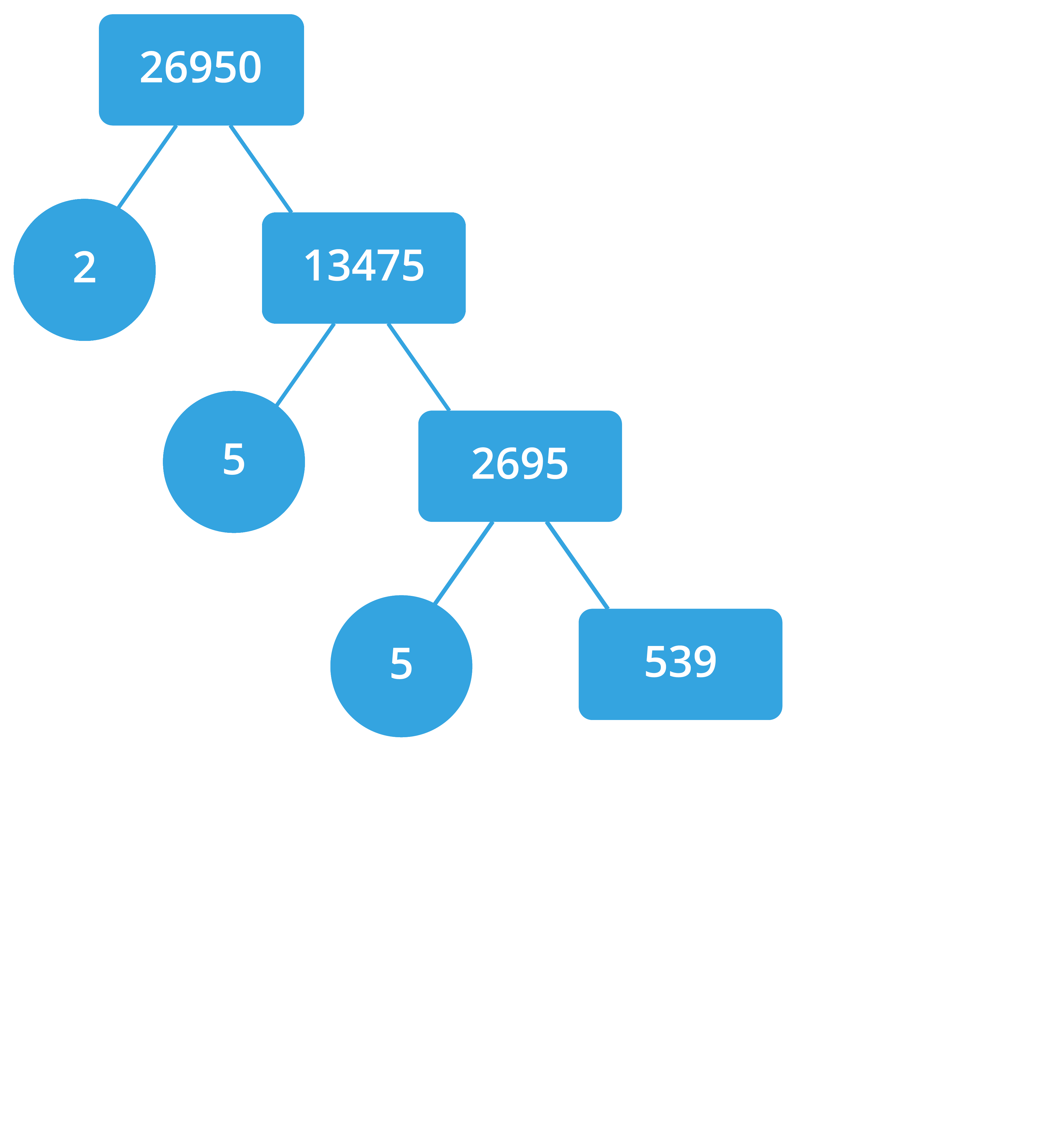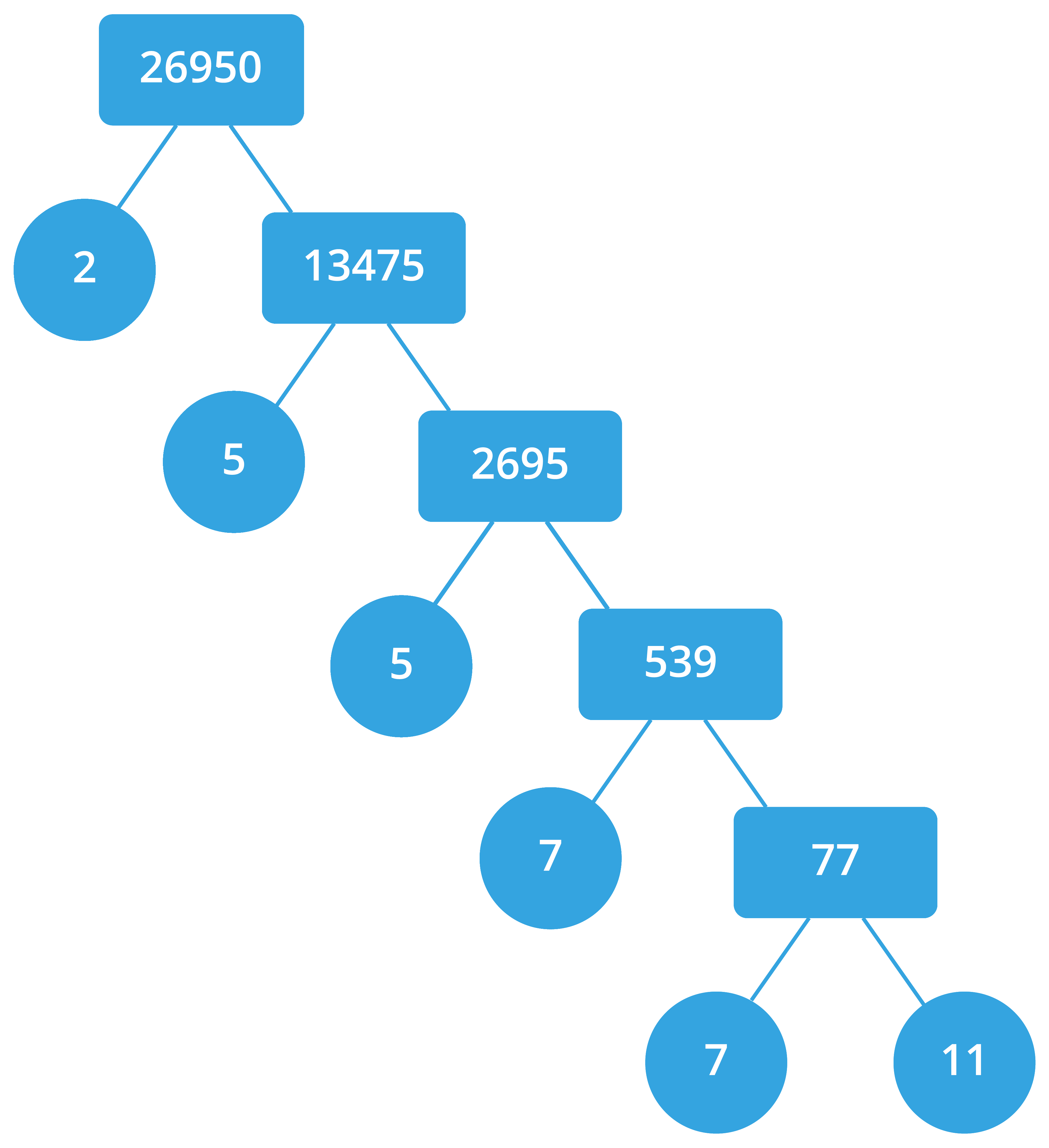
The prime factor of \(26950\) \(=\) \(2 \times 5 \times 5 \times 7 \times 7 \times 11\).
That is, \(26950 = 2 \times 5^2 \times 7^2 \times 11\).
Here, a composite number \(26950\) is written as a product of prime numbers.
If we change the order of the prime numbers, then also the answer will be the same composite number.
We can write \(26950 = 2 \times 7^2 \times 5^2 \times 11\) or \(26950 = 11 \times 7^2 \times 5^2 \times 2\).
Thus, the prime factorisation of a natural number is unique, except for the order of its factors.
Significance of the fundamental theorem of arithmetic
1. If a prime number \(p\) divides \(ab\), then \(p\) divides either \(a\) or \(b\). That is, \(p\) divides at least one of them.
Example:
Let us take a prime number \(3\) divides \(5 \times 6\).
Here, \(3\) cannot divide \(5\), but it divides \(6\).
That is, a prime number \(p\) divides at least one of them.
2. If a composite number \(n\) divides \(ab\), then \(n\) neither divide \(a\) nor \(b\).
Example:
Let us take a composite number \(4\) divides \(2 \times 6\).
Here, \(4\) neither divide \(2\) nor divide \(6\). But, it divides the product of \(2 \times 6 = 12\).
Thus, if a composite number \(n\) divides \(ab\), then \(n\) neither divide \(a\) nor \(b\).
Important!
Recall:
HCF \(=\) Product of the smallest power of each common prime factor in the numbers.
LCM \(=\) Product of the greatest power of each prime factor involved in the numbers.