PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoIn our day-to-day life, we come across a wide range of objects in the form of a combination of two or more solid shapes.
Let us discuss some real-life examples in this article where we can find the combination of one or more solids and learn how to find their volumes.
1. Capsule
The capsule is a combination of two solids, cylinder and hemisphere.
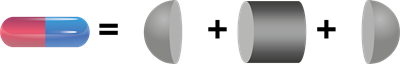
2. Circus tent
The circus tent is a combination of a cone and a cylinder.
3. Lollipop
The lollipop is a combination of a sphere and a cylinder.
Example:
The glass in the form of a cylinder surmounted on a hemisphere has a uniform radius of \(4\) \(cm\) and, the height of the cylindrical part is \(7\) \(cm\). Find the capacity of the glass.
Solution:
The volume of the glass \(=\) Volume of the hemisphere \(+\)Volume of the cylinder
Volume of the glass \(=\) \(\frac{2}{3} \pi r^3 \) \(+\) \(\pi r^2 h\)
\(=\) \(\left[\frac{2}{3} \times \frac{22}{7} \times (4)^3\right]\) \(+\) \(\left[\frac{22}{7} \times (4^2) \times 7 \right]\)
\(=\) \(\left[\frac{2}{3} \times \frac{22}{7} \times 64\right]\) \(+\) \(\left[\frac{22}{7} \times 16 \times 7 \right]\)
\(=\) \(134.1\) \(+\) \(352\)
\(=\) \(486.1\) \(cm^3\)
Therefore, the capacity of the glass is \(486.1\) \(cm^3\).
Register for free to see more content