UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreTwo triangles are similar; if
(i) their corresponding angles are equal, and
(ii) their corresponding sides are in the same ratio (or proportion).
Consider two triangles \(ABC\) and \(PQR\) are similar. Then,
(i) \(\angle A = \angle P\), \(\angle B = \angle Q\) and \(\angle C = \angle R\) and
(ii) \(\frac{AB}{PQ} = \frac{BC}{QR} = \frac{AC}{PR}\)
A Greek mathematician Thales put forward an interesting statement regarding two equiangular triangles which is "The ratio of any two corresponding sides in two equiangular triangles is always the same".
This result is called as "Basic proportionality theorem" or "Thales Theorem".
Using an activity, let us understand the basic proportionality theorem.
Activity:
Draw any angle \(XAY\) and mark points (say \(5\)) \(P_1\), \(P_2\), \(D\), \(P_3\) and \(B\) on the arm \(AX\) such that \(AP_1 = P_1P_2 = P_2D = DP_3 = P_3B\).
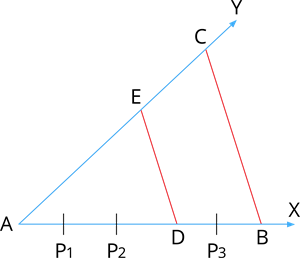
Through \(B\), draw a line intersecting the other arm \(AY\) at \(C\). Also, through \(D\), draw a line parallel to \(BC\) intersecting \(AC\) at \(E\).
Observe that, \(\frac{AD}{DB} = \frac{3}{2}\)
Also, \(\frac{AE}{EC} = \frac{3}{2}\)
Thus, in \(\triangle ABC\), \(DE \parallel BC\), then \(\frac{AD}{DB} = \frac{AE}{EC}\)
This result is proved as a theorem known as basic proportionality or Thales theorem.
Register for free to see more content