6. Examples

1. In a \(\triangle ABC\), a straight line \(DE\) intersects \(AB\) at \(D\) and \(AC\) at \(E\) and is parallel to \(BC\), then prove that \(\frac{AB}{AD} = \frac{AC}{AE}\)

 

Solution:

 

 

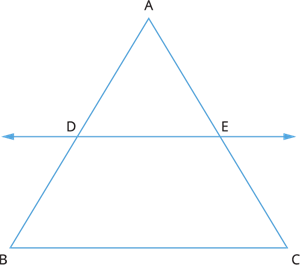
By Thales theorem, we have:

 

\(\frac{AD}{DB} = \frac{AE}{EC}\)

 

\(\frac{DB}{AD} = \frac{EC}{AE}\)

 

Adding \(1\) on both sides of the equation, we have:

 

\(\frac{DB}{AD} + 1 = \frac{EC}{AE} + 1\)

 

\(\frac{DB + AD}{AD} = \frac{EC + AE}{AE}\)

 

\(\frac{AB}{AD} = \frac{AC}{AE}\)

 

Hence, we proved.

 

 

2. In a \(\triangle ABC\), \(D\) and \(E\) are points on \(AB\) and \(AC\) respectively such that \(\frac{AD}{DB} = \frac{AE}{EC}\) and \(\angle ADE = \angle DEA\). Prove that \(\triangle ABC\) is isosceles.

 

Solution:

 

 

Given that \(\frac{AD}{DB} = \frac{AE}{EC}\), then by the converse of Thales theorem, we have:

 

\(DE \parallel BC\)

 

Therefore, \(\angle ADE = \angle ABC\) [Corresponding angles] ---- (\(1\))

 

and \(\angle DEA = \angle BCA\) [Corresponding angles] ---- (\(2\))

 

But, it is given that \(\angle ADE = \angle DEA\) ---- (\(3\))

 

Using (\(1\)) and (\(2\)) in equation (\(3\)), we get:

 

\(\angle ABC = \angle BCA\)

 

Therefore, \(AC = AB\) [If opposite angles are equal, then opposite sides are equal.]

 

Thus, \(\triangle ABC\) is isosceles.

 

Hence, we proved.