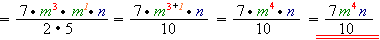Operations with monomials as fractions — lesson. Mathematics CBSE, Class 7.

UPSKILL MATH PLUS

Learn Mathematics through our AI based learning portal with the support of our Academic Experts!

When performing operations with monomials as fractions, the mathematical transformations are the same as in common fractions.

Example:

Add the monomials

\frac{5 x^{2} y}{4} + \frac{7 x^{2} y}{4}

1) Add the expressions in the numerators.

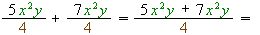
2) If possible, reduce the numeric factors of the numerator and the denominator.

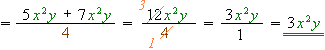
Example:

Subtract the monomials

\frac{a^{4} b^{2}}{8} - \frac{2 a^{4} b^{2}}{3}

1) Make denominators the same.

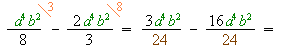
2) Subtract the expressions in the numerators.

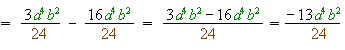
This fraction cannot be simplified.

Example:

Multiply the monomials

\frac{7 m^{3}}{2} \cdot \frac{mn}{5}

1) When multiplying the fractions, multiply the numerators and multiply the denominators.

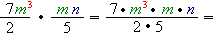
2) Multiply the variables by adding their exponents. Remember: if the exponent of a variable factor is not specified, then it is \(1\).

Did you find an error?

7. Operations with monomials as fractions