Addition and subtraction of monomials — lesson. Mathematics CBSE, Class 7.

PDF chapter test TRY NOW

Only the like terms can be added and subtracted. We can also say: only similar monomials can be added and subtracted.

Similar monomials are the monomials that have the like products of the variable terms, even if the terms' order is different.

To add or subtract monomials, the following steps must be followed:
1) add or subtract monomial coefficients;

2) do not change the variable factors.

Example:

\(2a + 8a = (2 + 8)a =10a\)

\( (2\) oranges \(+ 8\) oranges \(= 10\) oranges\( )\)

\(4b + b = (14 + 1)b = 15b\)

\( (14\) bananas \(+ 1\) banana \(= 15\) bananas\( )\)

\(114c - c = (114 - 1)c = 113c\)

\( (114\) lemons \(+ 1\) lemon \(= 113\) lemons\( )\)

2 x^{3} + 3 x^{3} = 5 x^{3}

4 a b^{2} - a b^{2} = 3 a b^{2}

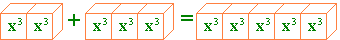
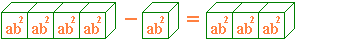
Important!

When adding or subtracting multiple monomials, keep in mind:

monomer coefficients are usually added or subtracted mentally and the simplified sum is written down;
if monomials have different sum of coefficients, they cannot be added or subtracted;
the sum of the opposite monomials is always \(0\).

Example:

Remove the brackets and replace the signs (because the brackets are preceded by a 'minus' sign

- (-) = +

\begin{array}{l} - 2 p^{3} k - (- 6 p^{3} k) - p^{3} k \\ = - 2 p^{3} k + 6 p^{3} k - p^{3} k \\ = 6 p^{3} k - p^{3} k - 2 p^{3} k \\ = 3 p^{3} k \end{array}

3 uv - 2 u v^{2} = 3 uv - 2 u v^{2}

These monomials cannot be subtracted because the products of their variable factors are different.

2 b^{3} c - 2 b^{3} c = 0

The sum of the opposite monomers is always \(0\).

Did you find an error?

3. Addition and subtraction of monomials