PDF chapter test TRY NOW

3. Funadamental operations in fractions: Multiplication

Multiplication of a fractional number with another fractional number can be done in two steps:

Step 1: Multiply the numerators of the fractions to get the new numerator.

Step2: Multiply the denominators of the fractions to get the new denominator.

It can be represented as:

Product of two fractions = \frac{Product of numerators of the fractions}{Product of denominators of the fractions}

Number of negative fractions	Sign of new fraction
Even	\(+\)
Odd	\(-\)

Multiplication of a fraction using the operator 'of ':

Let us understand this with an example,

Ravi has \(20\) apples, and Ram has one-fifth of it. How many apples does Ram have?

\begin{array}{l} The number of apple Ram has = \frac{1}{5} of 20 \\ = \frac{1}{5} \times 20 = \frac{20}{5} \\ = 4 apples \end{array}

Multiplication of a fraction by a whole number:

Let us understand how to multiply a fraction and a whole number.

Example:

Mithra went to a supermarket, where she bought three \(1/4\) kgs of rice packet. What is the total kg of rice she bought totally?

Let, \(1/4\) kg of rice packet \(=\)

Total Kg of rice she bought can be illustrated as,

= \frac{3}{4} = 3 \times \frac{1}{4} = \frac{3}{4}

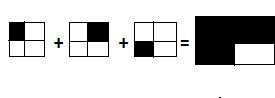
Multiplication of mixed fractions:

To multiply two mixed fractions first, convert them to improper fractions and then multiply the fractions.

Important!

Value of the products:

When two proper fractions are multiplied, the value of the product is less than each proper fraction.

When two improper fractions are multiplied, the value of the product is greater than each of the improper fraction.

Did you find an error?