PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoIntegers are the set of positive and negative numbers and zero. Even whole numbers are integers. Usually for better understanding integers are represented in a number line. Negative numbers will be on the left side of the number line, and positive numbers will be on the right side of the number line.
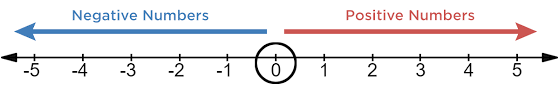
Example:
The examples of negative integers are \(-1, -2, -2199\).
The examples of positive integers are \(1, 38, 48, 122\).
The number \(0\) is neither negative nor positive.
Negative numbers are always lesser than zero and positive numbers.
Reflection of a number:
Reflection of a number will have the same absolute value as that number but with a different sign.
Example:
Reflection of \(-1\) is \(-(-1) = +1\)
Reflection of \(20\) is \(-20\)
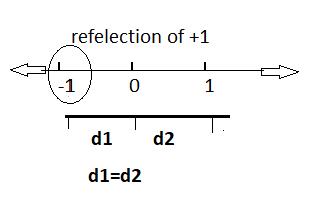
The distance between the positive number and zero in a number line will be equal to the distance between the reflection of the same negative number and zero.
Example:
Let us take a number \(+1\) its distance in the number line from \(0\) is \(1\).
Reflection of \(+1\) will be \(-(1)\) and its distance in the number line from \(0\) is also \(1\).
Distance between \(-20\) and \(0\) is \(20 =\) Distance between \(20\) and \(0\).
Important!
Numbers with decimals \((0.21, 2.35)\), Irrational numbers \(π≈3.14\), \(square\) \(roots - √2,√3\) are not integers.
Register for free to see more content