PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoLet us discuss what vertically opposite angles are.
Definition:
When two lines intersect at a particular point, the vertically opposite angles formed are equal in measure.
Illustration:
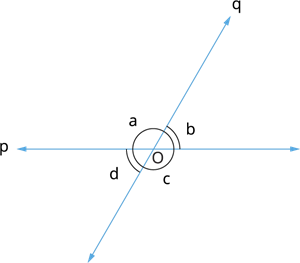
In the figure, the lines \(p\) and \(q\) intersect at \(O\) forming four pair of angles \(a\), \(b\), \(c\) and \(d\).
The angle \(a\) is vertically opposite to \(c\), and the angle \(b\) is vertically opposite to \(d\) and vice versa.
Here \(\angle a\) \(=\) \(\angle c\) and \(\angle b\) \(=\) \(\angle d\).
Let us prove the above equivalence as follows:
Consider \(\angle a\) and \(\angle b\).
These two angles form a linear pair. Hence by the property of linear pair of angles \(\angle a + \angle b = 180^{\circ}\).
\(\Rightarrow\) \(\angle a\) \(=\) \(180^{\circ}\) \(-\) \(\angle b\) ……\((1)\)
Also, \(\angle b\) \(=\) \(180^{\circ}\) \(-\) \(\angle a\) ……\((2)\)
Consider \(\angle b\) and \(\angle c\).
These two angles form a linear pair. Hence by the property of linear pair of angles \(\angle b + \angle c = 180^{\circ}\).
\(\Rightarrow\) \(\angle c\) \(=\) \(180^{\circ}\) \(-\) \(\angle b\) ……\((3)\)
Thus from equations \((1)\) and \((3)\) we have:
\(\angle a\) \(=\) \(\angle c\)
Similarly, consider \(\angle a\) and \(\angle d\).
These two angles form a linear pair. Hence by the property of linear pair of angles \(\angle a + \angle d = 180^{\circ}\).
\(\Rightarrow\) \(\angle d\) \(=\) \(180^{\circ}\) \(-\) \(\angle a\) ……\((4)\)
And from equations \((2)\) and \((4)\) we have:
\(\angle b\) \(=\) \(\angle d\)
Therefore, the vertically opposite angles formed by the lines \(p\) and \(q\) at the point \(O\) are equal in measure.
Example:
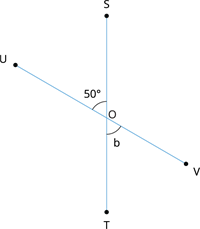
Find the unknown angle \(b\) in the figure.
Solution:
From the figure, we observe that the \(\angle SOU\) and \(\angle TOV\) are vertically opposite angles formed by the line segments \(ST\) and \(UV\).
By definition, the vertically opposite angles are equal.
Thus \(\angle SOU\) \(=\) \(\angle TOV\).
\(\Rightarrow\) \(b\) \(=\) \(50^{\circ}\)
Therefore, the unknown angle \(b\) is \(50^{\circ}\).
Register for free to see more content